Последната редакция на тази книга е от 2021 година.

I.8. Многофункционална комбинационна схема (управляем суматор)

Логически структури на устройства изградени от еднофункционални възли се наричат структури с разпределена операционна логика. Разпределената операционна логика причинява увеличаване на схемната част, но позволява повишаване на бързодействието, чрез възможността за паралелна работа на възлите.

Алтернатива на логическите структури с разпределена операционна логика, са структурите изградени върху многофункционални операционни възли, съсредоточаващи в себе си възможността за изпълнение на множество операции (или микрооперации). Тази алтернатива води до по-малки апаратурни разходи, но и до снижаване на бързодействието на устройствата.

Многофункционалните операционни възли най-често се реализират като комбинационни логически схеми и структурите, в които се използуват се наричат схеми със съсредоточена операционна логика. Настройката към определена операция се постига с допълнителна управляваща комбинация S, както е показано на фигура I.10, поради което такава схема може да се нарече управляема. Основните характеристики на такъв многофункционален операционен възел са: дължина на операндите и брой на реализируемите операции. Като завършен логически елемент тези схеми трябва да позволяват реализиране на възли с произволна дължина при съхраняване на операционното множество. Типичната дължина на входните операнди е 4, 8, 16 [b].

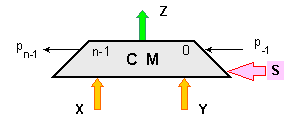
Фиг. I.10 Управляем суматор

Типичните операции, които се влагат, могат да бъдат разделени на две групи:

- логически (ляво/дясно изместване, логическо И, ИЛИ, НЕ, Mod2 и др.);

- аритметически (събиране, изваждане, преобразуване, +1, -1, поразрядно умножение и др.).

Ако на управляващата шина S се гледа като на управляващ код, то изходната функция може да се представи от дизюнкцията

Най-тривиалната реализация на тази функция е мултиплексиране на резултатите от множеството изпълними операции Z^(k) на изхода на схемата чрез кода S_k . На практика обаче оптимални схемни решения се получават чрез прилагане на методиките за проста разделителна функционална декомпозиция или за проста неразделителна функционална декомпозиция на логическите функции. И двата вида декомпозиция произлизат от правилата за функционална декомпозиция на Шенон върху множеството елементарни логически функции, определено във вида:

Споменатите методики за функционална декомпозиция следва да са познати на читателя, ето защо няма да се разкриват тук.

Конкретно полученото схемно решение не е универсално - то не може да се разширява. Типичен представител на този подход представлява интегралната схема 74181, в която реализираните микрооперации са 32 на брой, в зависимост от 5-разрядния управляващ код S. В таблица I.3 са представени уравненията на едноразряден изход от тази интегрална схема. Читателят следва да интерпретира правилно записаните уравнения, в които са употребени знаци както за логически така и за аритметически действия.

На фигура I.11 е представена принципната логическа схема на един (обобщен) разряд от многофункционална схема, реализираща операциите от таблица I.3.

Таблица I.3 Функции на изхода

	Логически операции S4=1	Аритметически операции S4=0
S3 S2 S1 S0		=1	=0
0 0 0 0	Z = X	Z = X	Z = X + 1
0 0 0 1	Z = X Ç Y
0 0 1 0		Z = X + X Ç Y	Z = X + X Ç Y + 1
0 0 1 1	Z = 0	Z = X + X	Z = X + X + 1
0 1 0 0	Z = X È Y	Z = X È Y	Z = X È Y + 1
0 1 0 1	Z = Y
0 1 1 0	Z = X Å Y	Z = X + Y	Z = X + Y + 1
0 1 1 1		Z = X È Y + X	Z = X È Y + X + 1
1 0 0 0
1 0 0 1		Z = X - Y - 1	Z = X - Y
1 0 1 0
1 0 1 1
1 1 0 0	Z = 1	Z = - 1	Z = 0
1 1 0 1
1 1 1 0		Z = X Ç Y - 1	Z = X Ç Y
1 1 1 1		Z = X - 1	Z = X

Следващите две таблици са помощни. Те представят логическите стойности, достигащи входовете на полусуматора в първото ниво на схемата, в зависимост от управляващия код.

S3	S2	b	S1	S0	a
0	0	X	0	0	0
0	1	X È Y	0	1
1	0		1	0	X Ç Y
1	1	1	1	1	X

Първото ниво от схемата има три изхода - полусумата от логически преработените операнди, функцията за генериране на преноса G_i, условието за разпространение на преноса R_i. Функцията на полусумата от това ниво обработва цифрите на двата операнда и се подава на третото ниво, където се формира крайният резултат с отчитане на преноса от предидущия по-младши разряд.

Обикновено, в конструктивно завършената група разряди се реализира функцията на преноса според зависимостта

където с i е означен номерът на разряда в групата, или с други думи групата разпространява паралелен пренос.

Във второто ниво действа разрядът S4 на управляващия код, който определя типа на операцията - логическа или аритметическа. При логическите операции не се разпространяват преноси.

Третото ниво на логическата схема формира окончателната сума.

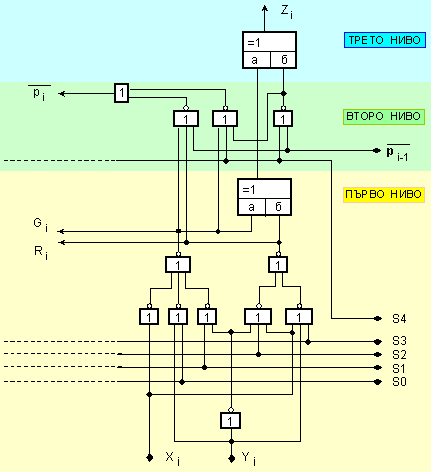
Фиг. I.11. Принципна логическа схема на едноразряден управляем суматор

Оценки и изводи: Подходът на групиране на разрядите по цялата дължина на суматора се оказва много плодотворен. Благодарение на неговото приложение (при математическия анализ на системата (22)) върху практическото разбиране за конструктивно завършени елементи, в схемите с паралелен пренос е отделен нов конструктивен елемент, наричан обикновено схема за ускорен пренос, основан на системата (25). Чрез него се постига висока степен на хомогенност при реализация на суматори с паралелен пренос при произволна дължина на разрядната мрежа.

На фигура I.12 е показана логическата схема на ИС от тип 74181, представляваща реализация на 4-разряден двоичен суматор с паралелен пренос. Както може да се види, схемата съответства на системата уравнения (23) и направените спрямо нея изводи в предидущия пункт.

Въпросът за разпространение на преносите между групите, при изграждане на суматор с по-голяма дължина, следва да се решава по начините и със средствата, които вече бяха описани.

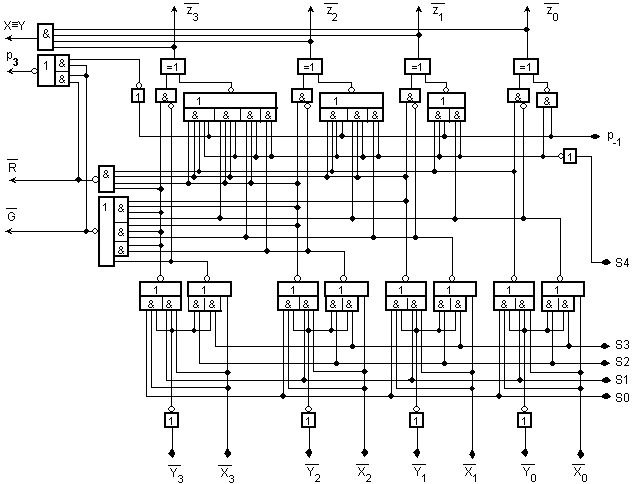
Фиг. I.12. Принципна логическа схема на ИС 74181

Въпроси и задачи:

1. Докажете и обяснете как са получени математическите изрази, вписани във всеки ред на таблица 3, като резултат на функцията на изхода Z, за всяка управляваща комбинация, при S4=0.

2. Докажете и обяснете как са получени математическите изрази, вписани във всеки ред на таблица 3, като резултат на функцията на изхода Z, за всяка управляваща комбинация, при S4=1.

3. Постройте 32-разряден управляем суматор чрез ИС 74181 и 74182 по структурата с паралелен пренос и оценете неговото бързодействие.

Следващият раздел е:

1.9 Ускоряване при едновременно събиране на повече от 2 числа