I.9.
Ускоряване
при
едновременно
събиране на
повече от 2
числа
Операция аритметическо събиране е двуместна операция, т.е. в нея участват 2 операнда. От техническа гледна точка обаче нищо не ни пречи да поставим въпроса за едновременно събиране на повече от 2 операнда, което е резонно, като имаме предвид математическите изрази с много операции.
Нека
като за
начало
разгледаме
случай на събиране
на 3 числа: (z=x1+x2+x3).
Изчислението
на тази сума
изисква
изпълнението
на 2
последователни
операции
събиране и
нейното
еднотактно
реализиране
с 2-входовите
суматори,
които бяха
изяснени и
синтезирани
в
предидущите
пунктове, ще
ни доведе до
следната
логическа
структура:
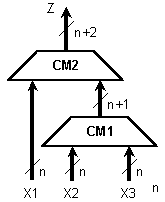
Фиг. I.13.
Последователно
събиране на 3
операнда
Преди
да
коментираме
времето за
превключване
на тази
структура
трябва да
обърнем внимание
на
разрядното
разширение
на междинния
и на
окончателния
резултат.
Това разширение
прави
суматорите
различни –
ако суматор СМ1
е n-разряден,
то суматор СМ2
трябва да е (n+1)-разряден.
Схемата
изисква
съответното
комутиране
на данновите
връзки.
Като
се позовем на
оценката на
времето за превключване
в пункт 1.4, че
закъснението
на n-битовата
сума е tS1=(n+1).t, а
на (n+1)-битовата
е
tS2=(n+2).t ,
то
максималното
закъснение
на крайния резултат
в горната
структура ще
бъде:
tS = tS1+ tS2 = (2.n+3).t , (32)
т.е.
двойно
по-голямо. Тази
оценка обаче
е с възможно
най-голямата
презастраховка.
Тя се получава
като се
изхожда от
разбирането,
че
събирането в
изходния
суматор
стартира след
формиране на
истинните
стойности на всички
цифри от
първата сума,
т.е след
превключване
на суматора СМ1.
На практика,
тъй като
схемата е
комбинационна,
готовите
младши цифри
на първата
сума
постъпват
веднага в суматор
СМ2, където в
младшите
разряди
започва
събиране с
вече
подадените
младши цифри
на събираемото
x1. Така
превключването
на изходния
суматор започва
със
закъснение 3.t
след
началото на
операцията и
протича в по-голямата
си част
паралелно
във времето с
превключването
на суматор СМ1.
Времевото
разположение
на двете
вериги от
последователно
разпространяващи
се преноси е
изобразено
на
следващата
рисунка:
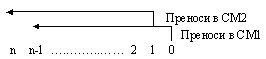
Фиг. I.14. Преноси
при последователно
събиране на 3
операнда
Така, с отчитане на паралелната работа на двата суматора, оценката на времето може да се прецизира и приема следния вид:
tS = 3.t+(n-1).t+t+3.t = (n+6).t
.
(33)
Нека анализираме по-подробно процеса на събиране, като го представим по следния начин:
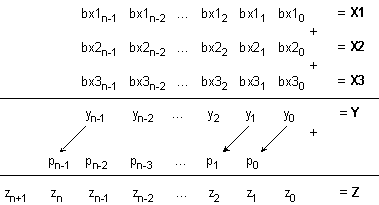
където
с bx1,
bx2, bx3 и
т.н. са
означени отделните
двоични
цифри на
числата x1, x2 и x3, а с Y и Z –
междинната и
крайната
суми
съответно.
От
схемата
по-горе се
вижда, че
междинната
сума Y може да се
получи като
поразрядна
без отчитане
на
възникналите
преноси при
събирането
на 3 цифри във
всеки разряд.
Технически тази
сума може да
се получи с
помощта на n на брой
пълни
едноразрядни
двоични
суматори,
наредени
един до друг
без всякаква
връзка между
тях. В същото
време
възникналите
от тези
суматори
преноси
(съответно
подредени
като (n+1)-разрядно
число) трябва
да се съберат
пълноценно
с междинния
резултат Y,
за което е
необходим
пълноценен
(разбирайте
пълен) n-разряден
двоичен
суматор, на
чийто изход
излизат
окончателните
стойности на
разрядите в
крайната
сума
Z = < zn+1 zn zn-1 … z2
z1 >.
Казаното
води до следната
структурна
схема:
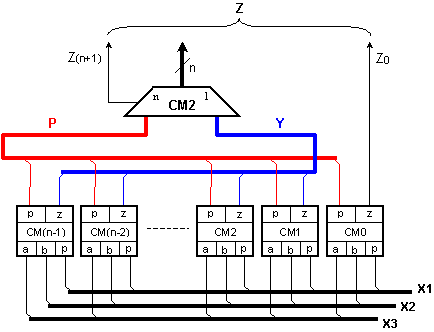
Фиг. I.15. Концентратор
(3:1)
Представената
схема е достатъчно
близка до
принципната
логическа и
позволява да
се определи
максималното
закъснение
на резултата.
Вижда се, че
всички цифри
на
междинната
сума Y
получават
истинните си
стойности
почти едновременно,
т.е. като
имаме
предвид
принципната
логическа
схема от фигура
I.2,
след
максимум 3.t
секунди. С t
е означено
времето за
превключване
на един
логически
елемент. Ако
суматорът СМ2
е изпълнен по
структурата
с ускорен
последователен
пренос, то ще
се добави още
и закъснението (n+2).t , така
окончателното
време за
превключване
на тази
структура ще се
оцени така:
tS = tS1+ tS2 = 3.t + (n+2).t
= (n+5).t .
(34)
Като
имаме
предвид, че
комутирането
на двата
суматора не е
оптимизирано,
тъй като не е
отчетено
какво точно
изисква на
вход за всеки
разряд
суматорът с
ускорен
последователен
пренос СМ2,
можем да
твърдим, че
така
получената
схема събира
3 числа 2 пъти
по-бързо от
представената
в началото
последователна
схема. Спрямо
паралелната
интерпретация
и нейната
оценка (33), то
оценката (34) е
почти
идентична.
Следващият
раздел е:
1.10.
Микроконвейерни
комбинационни
суматори