II. НАТРУПВАЩИ СУМАТОРИ
II.1.
Основни
положения
Двуместната
операция
събиране Z=X+Y в
много практически
ситуации се
среща като
натрупваща
се сума,
например при
изчисляване
на израза
Z=a+b+c+d+ … +f+k.
Когато
се изчислява
стойността
на подобен
израз, се
изпълнява
следната
линейна алгоритмична
схема:
Z := 0 ,
Z
:= Z + a ,
Z
:= Z + b ,
…………
Z := Z + f ,
Z := Z + k ,
в която
операция
събиране се
изпълнява последователно,
между всеки
следващ
операнд и
резултата
(междинната
сума) от
предидущото
събиране. В
този смисъл събирането
с натрупване
може да се
изрази така: Z=Z'+Y,
където Z' е
резултатът
от
предидущото
действие. В
този запис е
изразено
едно ново
разбиране, нова
характеристика
за
операцията - съхраняване
на резултата,
с цел
използуването
му като първи
операнд в
следващото
събиране. От
това следва,
че тук ще се
търси реализация
на логически
възел с две
възможности -
възможност
за запомняне
(възелът
следва да
притежава
свойство паметливост)
и възможност
за събиране.
В плана на
тези разсъждения
се вижда, че
бъдещият
логически
възел ще има един
многоразряден
вход и един
многоразряден
изход
(n-битови),
както е
показано на
фигура II.1. Тук,
както и във
всички
останали
случаи, се има
предвид
разрядна мрежа
с дължина n
бита, която
определя
техническите
параметри в
структурата
на възела. На
фигурата са показани
още
входящият
младши
пренос p-1
и
изходящият
старши
пренос pn-1, както и
управляващите
сигнали УС0 и УС1.
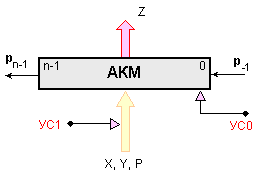
Фиг.
II.1.
Структурно
означение на
акумулатор
В
случаите,
когато
първият
операнд не е
резултатът
от
предидущото
събиране, то
той трябва
нарочно да
бъде внесен в
суматора като
такъв.
Последното
може да се
постигне чрез
предварително
нулиране
(изчистване)
на съдържанието
на суматора (Z=0),
с последващо
събиране Z=0+X.
Читателят
следва добре
да осмисли
появата на
необходимостта
от нулиране,
което представлява
микрооперация,
съществено
различаваща
се от
събиране.
Едва
след това
може да се
подаде
вторият операнд
и да се
получи
окончателната
сума
Z = Z'+Y = (0+X)+Y.
Възможността
да натрупва в
себе си
последователните
суми, дава
името на
суматора, който
още се
нарича акумулатор.
Вече
става ясно,
че операция
събиране във
възел с
такава
организация
ще се
изпълнява в
няколко
последователни
такта:
- първи
такт:
нулиране на
суматора Акм
:= 0;
- втори
такт:
подаване на
първи
операнд Акм
:=(Акм)+X = 0+X;
- трети
такт:
подаване на
втория
операнд Акм
:=(Акм)+Y = X+Y;
което
означава, че
изпълнението
на операцията
следва да се
управлява
във времето с
една логична
последователност
от
управляващи сигнали.
Като
се има в
предвид, че
се събират
числа, представени
в позиционна
бройна
система, трябва
да се
отбележи, че
при
последното
събиране (по
време на
трети такт) е
възможно
възникване
на преноси.
Събирането на
преносите с
вече
получената
междинна сума
следва да се
подчини на
съществуващата
организация,
което
означава, че е
необходим
още един,
последен
четвърти такт,
в който
възникналите
преноси ще
формират окончателната
сума: Акм:=(Акм)+{pi}.
От тук може
да се направи
извод, че
бъдещата
логическа
функция на
сумата е времева
логическа
функция !
Когато
се изпълнява
събиране, в
което предидущото
съдържание
на
акумулатора
се приема за
първи
операнд,
тогава
операцията
протича само
в последните
два такта
(трети и четвърти).
В
предидущата
тема беше
показано, че
паралелното
събиране на
многоразрядни
операнди,
представени
в позиционна
бройна система,
свежда
задачата за
синтез на
суматора до
синтез на
едноразряден
пълен
суматор. В
разглеждания
тук случай на
организация, операция
събиране в
текущия i-ти
разряд на
суматора
може да се
дефинира (по
време на
третия такт)
с таблица II.1:
Таблица
II.1
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Използвайки
дуализма,
който
осигурява двоичната
бройна
система,
интерпретираме
таблица II.1
като таблица
на истинност,
двоичните
цифри като
логически стойности
и функциите и
техните
аргументи като
логически.
Това ни дава
възможност
да търсим
техническата
реализация
на функциите
на суматора
чрез
методите и
средствата
на алгебрата
на логиката.
Логическите
функции на
сумата и
преноса, които
могат да се
запишат
аналитично в
СНДФ
(съвършена
нормална
дизюнктивна
форма) от
горната
таблица, имат
вида:
![]()
![]()
където с
буква t е означен
текущият
момент (такт).
Още веднъж
припомняме,
че става дума
за третия
такт.
Получените
логически
изрази
следва да се
минимизират.
Особеното
тук е, че на
минимизиране
следва да се
подложат
времеви
логически
функции, за
които
традиционните
методи в
алгебрата на
логиката не
могат да се
приложат. Ето
защо се анализира
въведената
организация.
Според
въведената
организация
за събиране,
истинните
стойности на
аргументите yi , pi-1, не
могат да
съществуват
на входа на
суматора
едновременно
във времето.
От това
следва, че
всяка тяхна
конюнкция е равна
на нула
(вечна 0; 0 във
всеки един
момент), т.е.
всички
минтерми в
горните
изрази,
съдържащи
логическото
произведение
(yi∩pi-1), се
признават за
равни на
логическа
константа
нула (yi∩pi-1=0). В
резултат
уравненията (35) и (36)
приемат вида:
![]()
![]()
Освен
конюнкцията
от правите
стойности на
втория и
третия
операнд (yi∩pi-1), следва
да се
анализират и
останалите
им съчетания,
имащи място в
уравненията
(37) и (38), а
именно:
![]()
За
тези
конюнкции,
въз основа на
описаните вече
разбирания и
организация,
може да се
докажат
следните
стойности за
всеки един
момент от
времето:
![]()
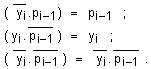
Тогава
след
заместване,
за функциите
на суматора
се получават
следните
изрази:
![]()
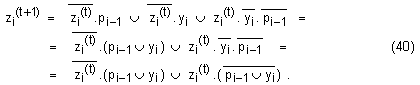
Ако
се положи
![]()
то
уравнението
на функцията
на сумата ще
приеме
окончателно
следния
минимален
вид:
![]()
а
уравнението
на функцията
на преноса
вида:
![]()
Уравненията
(41) и (42)
изразяват
аналитично
едноразрядния
двоичен
натрупващ
суматор.
Реализацията
на
логическото
уравнение на
сумата (41) се
осъществява
от
логическата
схема на T-тригер,
тъй като то
напълно
съответствува
на неговата
изходна
функция.
В
резултат, по
така
синтезираните
логически
функции, се
реализира
логическата
схема на едноразрядния
натрупващ
суматор,
показана на
фигура II.2.
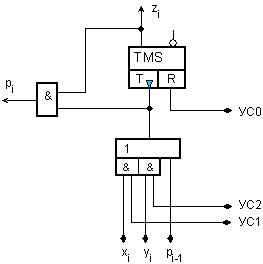
Фиг.
II.2. Принципна
логическа
схема на едноразряден
натрупващ
суматор
За
да се
реализира
правилно
уравнение (41) е избран
тригер със
структура MS,
който се превключва
по задния
фронт на
входните
импулси. За
целта
Т-входът на
тригера е
означен с
подходящ указател
(вижте
книга [3]).
Необходимо
е да се
отбележи, че
истинната стойност
на
логическата
функцията на
преноса (42) съществува
само в
момента на
управляващия
сигнал УС2, т.е. в
момента,
когато чрез
управляващият
сигнал УС2 (виж
фигура II.2) се
подава
истинната
логическа
стойност на
втория
операнд - yi. В този
смисъл
твърдим, че
преносът в
натрупващия
суматор има импулсен
характер и
той
съществува
само по
времето на подаване
на втория
операнд.
С така получената принципна логическа схема на едноразряден натрупващ суматор, чрез нейното мултиплициране и последователно свързване, е възможна реализацията на натрупващ суматор с произволна дължина.
Следващият
раздел е:
2.2
Многоразряден
двоичен
натрупващ суматор
с
последователен
пренос