II.2.
Многоразряден
двоичен
натрупващ суматор
с
последователен
пренос
Паралелното
събиране на
многоразрядни
операнди се
осъществява
с логическа
схема, изградена
от
необходимия
брой
едноразрядни
суматори,
свързани
помежду си
последователно,
както е
показано на
фигура II.3. В
тази схема разпространението
на преносите
според включването
им е
последователно.
Поради факта,
че
стойността
на преноса
възниква по
времето на
сигнала УС2,
когато
входовете Т
на тригерите
са заети от
втория
операнд, се
налага
допълнителното
включване на
логическите
елементи,
означени с
буква F. Задачата
на тези
елементи е да
изпълнят задържане
във времето
на истинната
стойност на
преносите
така, че те
попадат на
входовете Т
на всеки
следващ
тригер след
изчезване от
там на цифрите
на втория
операнд,
което се
налага от
възприетата
организация
за изпълнение
на операция
събиране.
Закъснелите
във времето
преноси са
означени със
знак плюс (p+i).
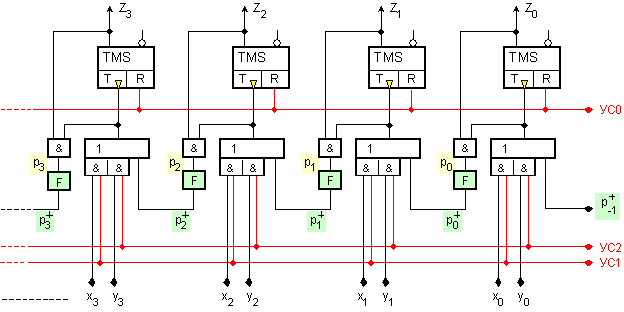
Фиг. II.3. Принципна
логическа
схема на натрупващ
суматор с
последователен
пренос
Функционирането
на логическа
схема, в която
има
запомнящи
логически
елементи
(тригери), при
изпълнение
на
алгоритмична
последователност
от
управляващи
сигнали, е
невъзможно
да бъде изследвано
без
построяване
на
времедиаграма
за нейното
превключване.
Ето защо
изследването
на суматора
от горната
схема ще бъде
свързано с
построяването
на
времедиаграмата
за неговото
превключване,
при
това за онзи
случай на
събиране, в
който
възникват
най-интересните
и
продължителни
превключвания.
Такъв е всеки
случай,
когато при
събиране на
две числа се
появяват
преноси във
всички
разряди. За
пример тук са
избрани
числата X=7 и Y=1.
Резултатът
от това
събиране е Z=8 и
той се
получава след
разпространение
на двоичен
пренос от
разряд №0 до
разряд №3. Процесът
на
получаване
на този
резултат е
представен
на
времедиаграмата
от фигура II.4. В началото
на
времедиаграмата
(фигура II.4) е изобразено
завареното
съдържание
на суматора
(Z=XXXX), останало
от предидущо
събиране.
Това
състояние на
суматора не е
известно и
тъй като
изпълнението
на операцията
ще бъде
представено
с
предварително
нулиране, то
не ни
интересува.
Вижда се, че
процесът
протича
както вече
беше описано
– нулиране по
УС0, подаване
на първи
операнд X по
УС1, подаване
на втори
операнд Y по
УС2 и разпространение
на преносите.
По време на
разпространение
на преносите управляващи
сигнали не се
подават.
Това
положение
дава
основанието
този последен
(четвърти)
такт да се
нарича празен
(виж фигура II.5).
Построената
за
събирането
на числата (7+1)
времедиаграма,
позволява да
се оцени
времето за превключване
на суматора в
последния
четвърти
такт, когато
се
разпространяват
преносите и
се формира
окончателната
сума. Както
се вижда от
фигура II.4,
продължителността
на
разпространяващите
се преноси е
равна на
продължителността
на
управляващия
сигнал УС2.
Характерното
за това
разпространение
е, че то е лавинообразно.
Обобщавайки
този случай
за първите
три разряда
на n-разряден
суматор,
времето за
неговото
превключване
се оценява
така
![]()
където
с t е означено
времето за
превключване
на Т-тригера.
Времедиаграмата
позволява да
се определи
стойността
на
закъснението,
което следва
да реализира
схемата на
елемента F от
фигура II.3.
Закъснението
има стойността:
![]()
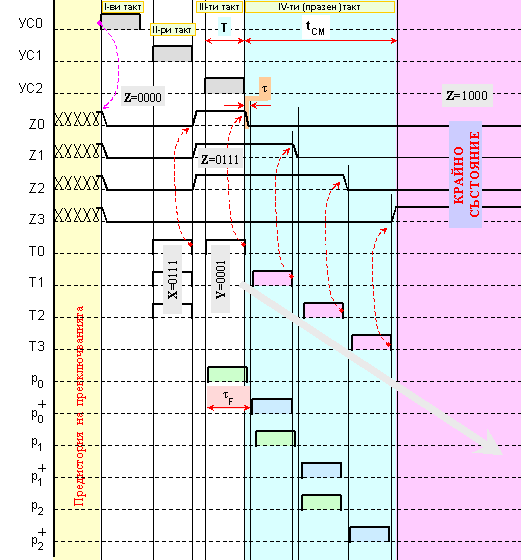
Фиг. II.4. Събиране
(7+1) в натрупващ
суматор с
последователен
пренос
Вижда се
още, че
основната
част на това
закъснение
се формира от
продължителността
Т на
управляващия
сигнал УС2. От
анализа на това
закъснение
може да се
стигне до
извода, че
неговата
реализация
може да се
осъществи
чрез D-тригер.
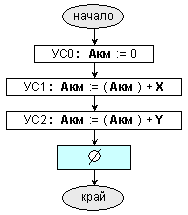
Фиг. II.5. Блок-схема
на
алгоритъма
за събиране в
натрупващ
суматор
На фигура II.6 е показана окончателната реализация на натрупващия суматор с последователен пренос.
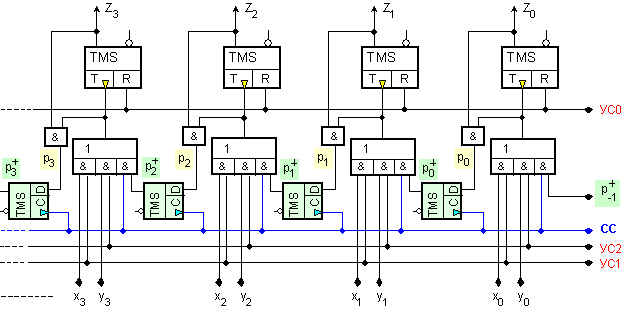
Фиг. II.6. Принципна
логическа
схема на натрупващ
суматор с
последователен
пренос
Схемата
от фигура II.6
работи при
условие, че управляващите
сигнали УС0, УС1 и УС2
са
стробирани
със сигнала CC,
с други думи
периодът на
синхронния
сигнал TCC определя
продължителността
на управляващите
сигнали (TCC=TУC).
Читателят
следва да
обърне
внимание на
D-тригерите,
които също
както и
Т-тригерите,
се
превключват
по заден
фронт.
Въпроси и
задачи:
1.
Постройте
времедиаграма
за събиране
на числата 3 и 6,
при което се
постарайте
да обосновете
оценката на
времето за
задържане на преносите tF.
Разгледайте
и други
примери, така
щото при
събиране да
се появяват
както
транзитни, така
и местни
преноси.
Направете
изводи за
превключването
на суматорите.
2.
Докажете в
какво
съотношение
следва да се намират
времето за
превключване
tT на
Т-тригера и
времето за
превключване
tD на
D-тригера.
Обосновете
надеждността
на схемата.
3.
Постройте
времедиаграма
за същия
пример за
схемата от
фигура II.6 и сравнете.
Изведете
изисквания
към
коефициента
на запълване
на тактовата
последователност
СС.
4.
Възможна ли е
работа на
схемите при
употреба на
тригери,
превключващи
се по
предните фронтове
на входните
сигнали?
5.
Възможна ли е
работа на
схемата от
фигура II.6 при
употреба на
тригери,
превключващи
се по предния
фронт на
сигнала CC?
6.
Какъв е
ефектът от
скъсяване на
продължителността
на
управляващия
сигнал УС2 в
резултат от
стробирането
и каква е
неговата
минимална
стойност?
Формализирайте
условията за
постигане на
максимално
бързодействие
на представените
по-горе
натрупващи
суматори.
Следващият
раздел е:
2.3
Многоразряден
двоичен
натрупващ
суматор с
транзитен
пренос