II.4.
Двутактов
натрупващ
суматор
Съществен
недостатък
на
суматорите с
последователен
и транзитен
пренос е
необходимостта
от въвеждане
във всеки
разряд на схема
за задържане
на преноса.
Реализацията
на тези n на
брой схеми
чрез
двутактов
D-тригер с
отчитане на
спецификата
на неговото управление
увеличава
двойно
апаратните
разходи за
суматора.
Анализирайки
последната
схема на
суматора (виж
фигура II.7),
естествено
възниква
желанието за
отстраняване
на схемите за
задържане на
преноса за
всеки разряд
поотделно.
Преследвайки
това желание
се стига до следната
идея -
необходимостта
от задържане
на преноса може
да бъде
отстранена, ако
неговото
изчисление
се пренесе в
следващия
момент.
Задържането
на преноса в
предидущата схема
(фигура II.7) се
налага по
причина на
това, че
неговата
истинна
стойност се
изчислява в
момента,
когато се
подава
втория
операнд и тъй
като
суматорът
има един
вход, който в
този момент е
зает, то се
налага
задържане на
вече
получената стойност.
С други думи
изчислението
на истинната
стойност на
преноса
следва да се
отложи и да
се направи в
момента
отреден за
неговото
разпространение,
т.е.
четвъртия
такт.
В
момента на
четвъртия
такт обаче,
безвъзвратно
във времето
са отминали
както моментът
на подаване
на първия
операнд, така
и моментът на
подаване на
втория
операнд, т. е. в този
такт не се
разполага с
истинните
стойности
нито на
първия, нито
на втория
операнд. По
това време
единствената
информация, която
съществува в
суматора, е
полусумата
от двата
операнда X+Y.
Стойността
на тази
полусума се
намира на правия
изход на
T-тригера.
При
това
положение,
реализирането
на идеята за
изчисление
на преноса в
четвъртия такт,
е възможно
само ако
първият и
вторият операнд
се подадат
повторно и в
този такт.
Повторното
подаване на
втория операнд
е възможно,
но
повторното
подаване на
първия е
невъзможно.
Невъзможно е
затова защото
в качеството
си на
резултат от
предидущо
действие, при
събирането си с
втория
операнд в
суматора, той
безвъзвратно
е изчезнал
и на негово
място в
Т-тригера се
намира
полусумата X+Y. От
казаното
следва, че
истинната
стойност на
първия
операнд
трябва да се
възстанови от
тази
полусума, а
втория
операнд да се
подаде
повторно.
Повторното
подаване на
втория
операнд е
причина за
наименованието
на този
суматор - двутактов.
И
така,
събирането в
първите три
такта протича
така, както и
в
предидущите
схеми, т.е. изчислява
се
полусумата
от първия и
втория операнд,
но без
отчитане на
преноса. В
последният
такт се
извършва
окончателното
формиране на
сумата.
Пълноценно
операция
събиране, при
тази
организация,
може да се
представи с
таблицата на
истинност II.2.
Таблица
II.2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
В
таблица II.2 по
това време,
вторият
операнд yi
се подава
повторно с
цел да се
изчисли
преносът pi, а
сумата
z(t)i
формира
окончателната
си стойност
след
отчитане на
преноса pi-1. В този
смисъл
колонката на
функцията на
сумата
z(t+1)i
се попълва
чрез втората
и четвъртата
колонка на
аргументите.
Попълването
на колонката
на функцията
на преноса се
извършва
чрез първата,
третата и
четвъртата
колонка на
аргументите. Специално
следва да се
поясни
съдържанието
на третата
колонка. Там
са
изобразени
възстановените
в предидущия
(t-1) момент
стойности на
сумата, които
по същество
представляват
стойностите
на първия
операнд - x,
т.е.
![]()
От
тази таблица
на истинност
се получава МДФ
на
логическата
функцията на
преноса като
функция от
онези
стойности на
аргументите, които
съществуват
едновременно
в този
момент, а
това са
стойностите
от първата,
втората и
четвъртата
колонки.
|
|
|
|
|
|
|
|
|
|
00 |
01 |
11 |
10 |
|
|
0 |
0 |
0 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
0 |
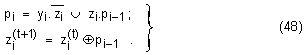
В
резултат на
изложения
синтез се
получава
логическата
схема за
двутактов
натрупващ
суматор,
представена
на фигура II.9:
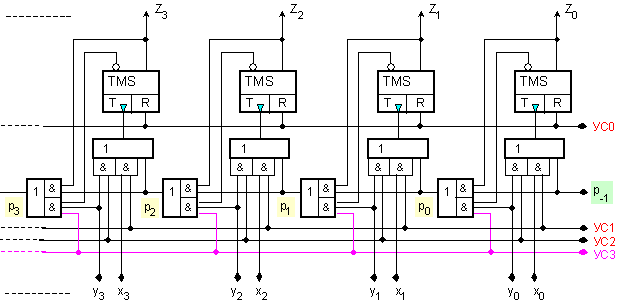
Фиг. II.9. Принципна
логическа
схема на
двутактов натрупващ
суматор
Логическата
схемата от
фигура II.9 е
схема на суматор
с
последователен
пренос. Тази
схема, за
разлика от
предидущите,
се управлява с
още един
управляващ
сигнал - УС3,
с помощта на
който
вторият
операнд y се
подава
повторно в
логическите
елементи за
изчисляване
на
преносите pi.
Функционирането
на схемата е
показано на времедиаграмата
от фигура II.10,
при събиране на
числата 5 и 3.
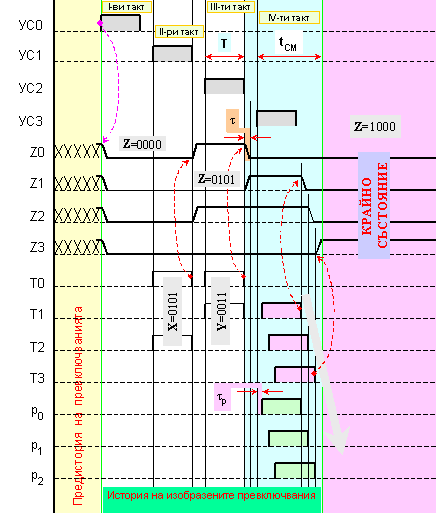
Фиг. II.10. Събиране
(5+3) в двутактов
натрупващ
суматор
Представената
на фигура II.10
времедиаграма
позволява да
бъдат
направени
редица изводи
и оценки.
Така
например,
върху нея се
вижда как
всички
преноси в
суматора (p0, p1,
p2) и т.н.
възникват не
по времето на
УС2, а
по времето на
УС3.
Разпространението
им е
последователно
и натрупването
на
последователните
закъсненията tp
са
неизбежни. На
времедиаграмата
те са
представени
силно
преувеличени.
Общата
оценка на
времето за
превключване
се дава с
формулата
![]()
т.е. това е
същото време
като при
суматор с транзитен
пренос (виж
уравнение (46)).
И тук,
както за
предидущите
схеми, може
да се постави
въпросът за
минимизиране
на времето за
превключване
на схемата
чрез скъсяване
продължителността
Т
за подаване на
втория
операнд.
Граничната
стойност, до която
може да падне
времето за
превключване
на суматора,
е следната:
![]()
По-нататъшното
повишаване
на
бързодействието
на така
синтезирания
натрупващ
суматор
следва да се
търси в
минимизирането
на втория
член на
сумата от
горната
формула. Това
е възможно да
се постигне
чрез всеки един
от подходите,
разгледани и
приложени за комбинационните
суматори.
Най-често
прилагания
подход е
организиране
на паралелно
разпространение
на преноса
както върху цялата
дължина на
суматора,
така и чрез
разделянето
му на групи.
Въпроси
и задачи:
1.
Постройте
пълната
времедиаграма
за работата
на 4-разряден
двутактов
натрупващ
суматор при
събиране на
числата X=5 и Y=7.
2.
Синтезирайте
4-разряден
двутактов
натрупващ
суматор с
паралелен
пренос.
3. Обяснете
защо
предният
фронт на
управляващия
сигнал УС3 трябва
да закъснява
минимум на [s] след
задния фронт
на сигнала УС2.
Дайте пример
за
доказателството.
Оценки и
изводи: Сравнявайки
оценките (37), (40) и
(49) на времето
за
превключване
на различните
суматори,
вече може да
се обобщи, че
от разгледаните
структури
последната е
най-добрата и
тя
действително
намира
практическо
приложение.
Това е така,
тъй като тя е
най-икономична
и най-бърза. Читателят
обаче следва
добре да
разбира, че
синтезът на
двутактовия
натрупващ
суматор не би
бил така
естествен,
ако той не
беше разгледан
тук в тази
последователност,
в която след
анализ на
качествата,
постигнати
във всяка от
предидущите
схеми, е
възприета и реализирана
най-ползотворната
идея.
Следващият
раздел е: