Последната редакция на тази книга е от 2021 година.

IV. ЧИСЛА С ФИКСИРАНА ЗАПЕТАЯ

IV.1. Общи положения

Представяните числа се интерпретират като числа без знак или като числа със знак. Разрядната мрежа, в която се представят двоичните числа с дясно фиксирана запетая (ДФЗ), има вид, който е определен в книга [1].

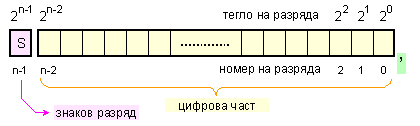
Двете числа:

определят диапазона на представимите в разрядната мрежа числа

Разрядната мрежа, в която се представят двоичните числа с ляво фиксирана запетая (ЛФЗ) има вид, който е определен в книга [1].

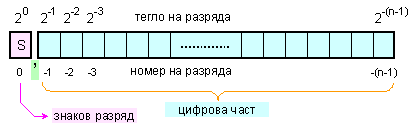
Двете числа:

определят диапазона на представимите в разрядната мрежа числа.

Числата със знак се представят в следните кодове - прав, обратен и допълнителен, които се дефинират по следния начин:

А) При дясно фиксирана запетая

Прав код:

Кодът нееднозначно представя числото нула, т.е.

[ +0 ]_ПК = 0000 ; [ -0 ]_ПК = 1000 , ако n=4[b].

Обратен код:

Кодът нееднозначно представя числото нула, т.е.

[ +0 ]_ОК = 0000 ; [ -0 ]_ОК = 1111 , ако n=4[b].

Допълнителен код:

Кодът еднозначно представя числото нула, в резултат на което разширява отляво с една единица (една стъпка или с един дискрет) диапазона на представимите числа. Например, при n=8[b] той е

[ -128 ¸ +127 ]₍₁₀₎ º [ 10000000 ¸ 01111111 ]_{(2) ДК} .

За инверсните кодове са в сила съотношенията:

Б) При ляво фиксирана запетая

Прав код:

Кодът нееднозначно представя числото нула, т.е.

[ +0 ]_ПК = 0000 ; [ -0 ]_ПК = 1000 , ако n=4[b].

Обратен код:

Кодът нееднозначно представя числото нула, т.е.

[ +0 ]_ОК = 0000 ; [ -0 ]_ОК = 1111 , ако n=4[b].

Допълнителен код:

Кодът еднозначно представя числото нула, в резултат на което разширява отляво с една стъпка (един дискрет) диапазона на представимите числа. Например, при n=4 [b] той е

[ -1 ¸ +0,875 ]₍₁₀₎ º [ 1000 ¸ 0111 ]_{(2) ДК} .

За инверсните кодове и тук са в сила съотношенията:

Числата се представят още и в модифицирани кодове (прав, обратен, допълнителен). Модифицираните кодове разширяват отляво разрядната мрежа с един допълнителен знаков разряд. Този разряд има номер n в разрядна мрежа с ДФЗ и номер 1 в разрядна мрежа с ЛФЗ.

ПРИМЕР 1. Да се представи в ПК, ОК, ДК, МПК, МОК и в МДК числото X=44 в разрядна мрежа с дължина n=8 [b].

X₍₂₎ = +101100 .

[X]_ПК = 0 0101100 ; [X]_ОК = 0 0101100 ; [X]_ДК = 0 0101100 ;

[X]_МПК = 00 0101100 ; [X]_МОК = 00 0101100 ; [X]_МДК = 00 0101100 ;

ПРИМЕР 2. Да се представят в ПК, ОК, ДК, МПК, МОК и в МДК числата

X = -44 и Y = -0,3965

в разрядна мрежа с дължина n=8 и n=10 [b] съответно.

X₍₂₎ = -101100 , Y₍₂₎ = -0,011001011 .

[X]_ПК = 1 0101100 ; [Y]_ПК = 1 011001011 ;

[X]_ОК = 1 1010011 ; [Y]_ОК = 1 100110100 ;

[X]_ДК = 1 1010100 ; [Y]_ДК = 1 100110101 ;

[X]_МПК = 11 0101100 ; [Y]_МПК = 11 011001011 ;

[X]_МОК = 11 1010011 ; [Y]_МОК = 11 100110100 ;

[X]_МДК = 11 1010100 ; [Y]_МДК = 11 100110101 .

Следващият раздел е:

4.2 Операции събиране и изваждане на числа с фиксирана запетая с препълване