IV.3 Операция умножение
За
извършване
на операция
умножение Z=X.Y на
числа с
фиксирана
запетая,
представени в
позиционна
бройна
система, се
прилагат два
основни
метода - за
умножение с
младшите
разряди
напред и за
умножение
със старшите
разряди
напред. Всеки
един от тези
методи може да
бъде
алгоритмизиран
или по
схемата с неподвижно
множимо, или
по схемата с
неподвижна
междинна
сума. Всяка
от
получените
четири схеми
за
организация
може да има
своите разновидности,
зависещи от
кода, в който
са представени
операндите.
Излишно е да
обясняваме,
че числата са
представени
в двоична
бройна
система.
Главна
обща
особеност на
операция
умножение е
удвоеният
формат на
резултата, по
отношение на
този на
операндите.
Всички
числени
примери са
изпълнени
във вид на
рисунка,
която зависи
от
логическата структура
на
съответното устройство
и на
разположението
на логическите
му възли в
нейната
схема. Всяка
такава
логическа
структура е
синтезирана
в пряка
връзка с
алгоритъма
на
съответната
аритметическа
операция, по
която тя
функционира.
Методите,
алгоритмите
и синтезът на
логическите
структури
читателят ще
намери в
съответните
раздели на книга [1]. Всеки
числен
пример, който
е представен
в тази книга,
има за цел да
илюстрира
съответния
алгоритъм. В
този смисъл
обаче той
демонстрира
и неговата
правилност,
както и
правилността
на самата
логическа
структура на
съответното
устройство.
Ето защо
примерите
нямат
самостоятелно
значение – те
са
илюстрация
на теорията,
синтеза и реализацията
на
съответното
устройство.
Това
означава, че
читателят
следва да
разглежда
книгите
съвместно.
В
разделът
по-долу са
илюстрирани
двата метода
за умножение,
според
схемата с
неподвижно
множимо.
Изборът на
тази схема за
изпълнение
на
операцията е
обоснован в книга [1]. Ще
обърнем
внимание, че
ръчното
умножение, което
познава
всеки от нас,
се изпълнява
по схемата с
неподвижна
междинна
сума.
IV.3.1
Умножение
на числа с
дясно фиксирана
запетая по
модул
А)
УМНОЖЕНИЕ С
МЛАДШИТЕ
РАЗРЯДИ НАПРЕД
ПО СХЕМАТА С
НЕПОДВИЖНО
МНОЖИМО
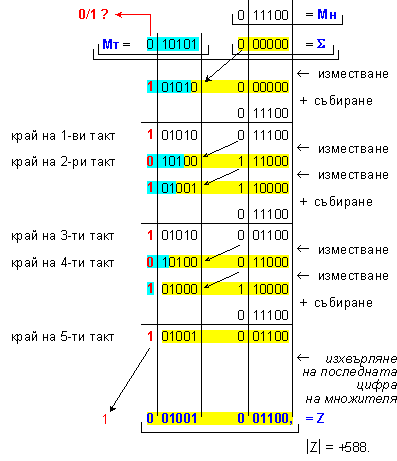
ПРИМЕР 49. Да
се изпълни
операция
умножение Z=X.Y на
числата X=28 и Y=21, които
са
представени
в разрядна
мрежа с дължина n=6[b].
|X| = 0 11100; |Y| = 0 10101
От
примера се
вижда, че на
всеки такт се
изпълнява
операция събиране
и изместване
или само
изместване, в
зависимост
от цифрите на
множителя.
Изместванията
са толкова,
колкото е n -
дължината на
разрядната
мрежа.
Форматът на
произведението
е 2.n.
При всеки нов
такт
младшите разряди
на
междинната
сума
навлизат в
полето на
изместващият
се множител.
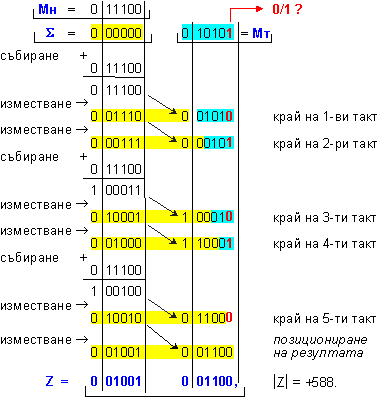
Б) УМНОЖЕНИЕ СЪС СТАРШИТЕ РАЗРЯДИ НАПРЕД ПО СХЕМАТА С НЕПОДВИЖНО МНОЖИМО
В тази схема изместванията предхождат събирането. Междинната сума при изместването си наляво навлиза в полето на множителя. Тук, за разлика от предидущата схема, събирането се извършва по цялата дължина на междинната сума - 2n разряда, чрез разпространяване на преноса от младшата й половина в старшата.
ПРИМЕР 50. Да се
изпълни
операция
умножение Z=X.Y
на числата X=28
и Y=21, които
са
представени
в разрядна
мрежа с дължина n=6[b].
|X| = 0
11100; |Y| = 0
10101