IV.3.5 Приложение на модифицираните кодове
Всички
алгоритми за
умножение,
използуващи
аритметическо
изместване
надясно, се сблъскват
с проблема
наречен “изчезване
на знака” при
препълване.
Решението на
този проблем
с помощта на
възстановяващата
функция S с
уравнение (95) не е
единствено.
Другото
решение е
прилагане на
модифициран
допълнителен
код за представяне
на
междинната
сума. В този
случай
знаковите
разряди на
сумата
служат както
за откриване
на
препълването,
така и за
запазване на
занака й. И
тъй като левият
знаков
разряд
винаги
съхранява истинската
стойност на
знака, то
става
ненужно да се
следи за
настъпване на
препълване.
Тогава
аритметическото
изместване
надясно,
което следва
след събиране,
може да се
изпълни в
чист вид, т.е.
по
определение,
спрямо левия знаков
разряд.
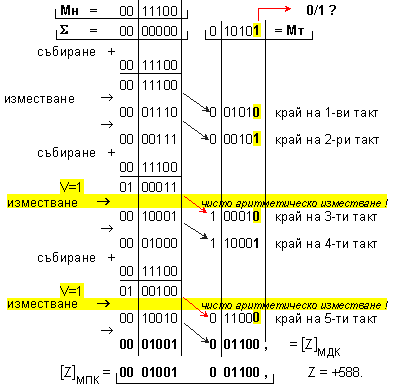
ПРИМЕР
63. Да се
изпълни
операция
умножение Z=X.Y на числата X=28 и Y=21, които са
представени
в разрядна
мрежа с дължина n=6[b], в
модифициран
допълнителен
код.
![]()
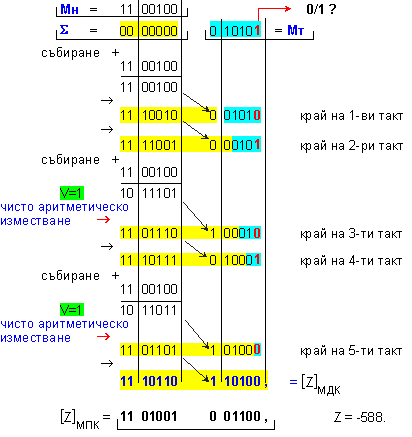
ПРИМЕР
64. Да се
изпълни
операция
умножение Z=X.Y на
числата X=-28 и Y=21, които са
представени
в разрядна
мрежа с дължина n=6[b], в
модифициран
допълнителен
код.
![]()
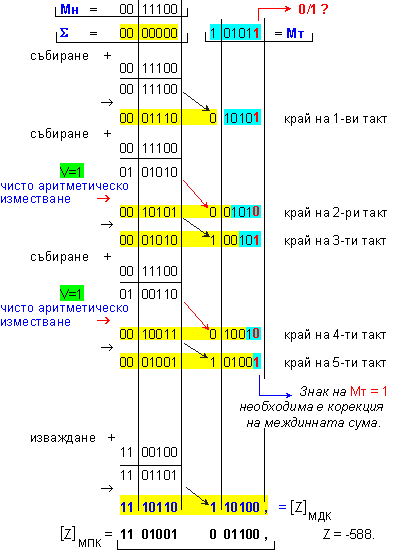
ПРИМЕР 65. Да се
изпълни
операция умножение Z=X.Y
на числата X=28 и
Y=-21, които
са
представени
в разрядна мрежа
с дължина n=6[b], в
модифициран
допълнителен
код.
![]()
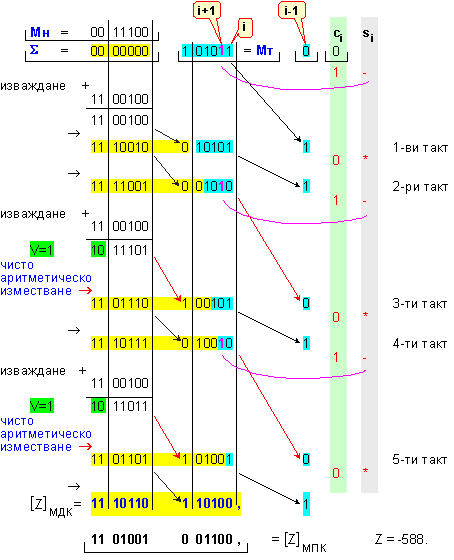
ПРИМЕР 66. Да се
изпълни
операция умножение Z=X.Y
на числата X=28 и
Y=-21, които
са
представени
в разрядна мрежа
с дължина n=6[b] в
модифициран
допълнителен
код по алгоритъма
на Леман.
![]()
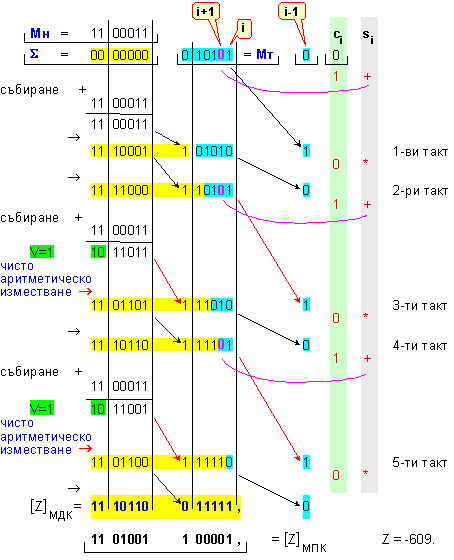
ПРИМЕР 67. Да се
изпълни
операция умножение Z=X.Y на
числата X=-29 и Y=21,
които са
представени
в разрядна
мрежа с дължина
n=6[b] в
модифициран
допълнителен
код по алгоритъма
на Леман.
![]()
Следващият
раздел е:
4.3.6
Умножение
на два
разряда
едновременно