Последната редакция на тази книга е от 2021 година.

IV.3.6 Умножение на два разряда едновременно

Умножението с два и повече разряда едновременно се отнася към групата алгоритми за апаратно ускоряване на операцията. Съществуват алгоритми за изпълнението й и по двата метода, както за числа без знак, така и за числа със знак, представени в допълнителен код.

А) УМНОЖЕНИЕ ПО МОДУЛ С МЛАДШИТЕ РАЗРЯДИ НАПРЕД, ПО СХЕМАТА С НЕПОДВИЖНО МНОЖИМО

Микрооперациите, необходими за изпълнение на всеки такт в този алгоритъм, се определят според цифрите на текущата вдойка разряди на множителя ( y_i+1, y_i) и функцията за корекция K_j-1 на междинната сума. С буква i е означен номерът на текущия разряд на множителя, а с буква j – номерът на текущата двойка разряди. Възможните ситуации са определени в таблица IV.1. Вижда се назначената за текущия такт операция и новата стойност на функцията за корекция K_j, която ще се отчита след изместването, заедно със следващата двойка разряди на множителя.

Таблица IV.1

			Операция
0	0	0	+ 0	0
0	0	1	+ Мн	0
0	1	0	+ 2.Мн	0
0	1	1	- Мн	1
1	0	0	+ Мн	0
1	0	1	+ 2.Мн	0
1	1	0	- Мн	1
1	1	1	+ 0	1

Наличието на операция (+2.Мн) налага междинните суми да се формират с един допълнителен разряд отляво.

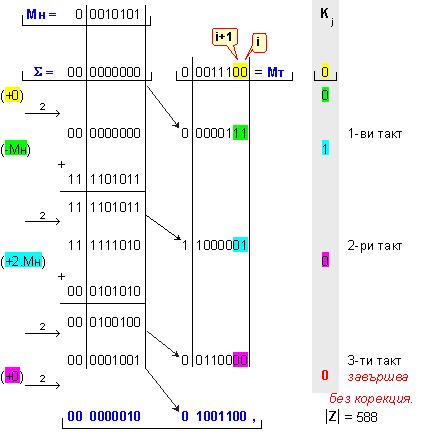
ПРИМЕР 68. Да се изпълни операция умножение Z=X.Y на числата X=21 и Y=28, които са представени в разрядна мрежа с дължина n=8[b], по метода с два разряда едновременно.

Мн = |X| = 0 0010101 ; Мт = |Y| = 0 0011100 .

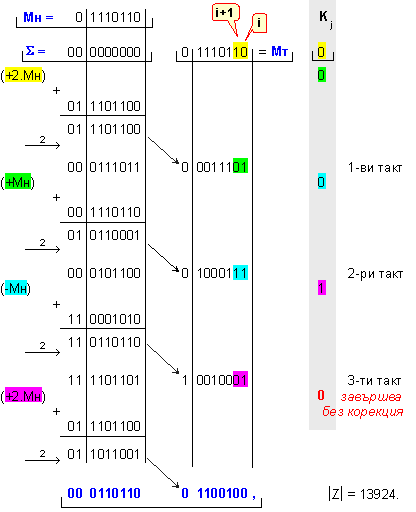
ПРИМЕР 69. Да се изпълни операция умножение Z=X.Y на числата X=118 и Y=118, които са представени в разрядна мрежа с дължина n=8[b], по метода с два разряда едновременно.

Мн = |X| = 0 1110110 ; Мт = |Y| = 0 1110110 .

Б) УМНОЖЕНИЕ ПО МОДУЛ С СТАРШИТЕ РАЗРЯДИ НАПРЕД, ПО СХЕМАТА С НЕПОДВИЖНО МНОЖИМО

В този алгоритъм микрооперациите, необходими за изпълнение на всеки такт, се определят според цифрите на текущата двойка разряди на множителя ( y_i, y_i-1) и функцията за корекция на междинната сума.

В случая ролята на тази функция се изпълнява от младшата цифра на преидущата двойка разряди на множителя ( y_i+1). Възможните ситуации са определени чрез таблица IV.2.

Таблица IV.2

			Операция
0	0	0	+ 0	0
0	0	1	+ 2.Мн	1
0	1	0	+ 2.Мн	0
0	1	1	+ 4.Мн	1
1	0	0	- 4.Мн	0
1	0	1	- 2.Мн	1
1	1	0	- 2.Мн	0
1	1	1	+ 0	1

Така както и при умножение с една цифра на множителя, в последния такт не се извършва изместване на междинната сума, а само на последните цифри на множителя, останали в неговия регистър. При този алгоритъм обаче, след умножение с последната двойка разряди на множителя, е възможно междинната сума да е формирана с излишък. Така че, ако младшата цифра на множителя в тази последна двойка се окаже единица, то е необходимо да се извърши последна коригираща операция - изваждане на множимото от текущата сума.

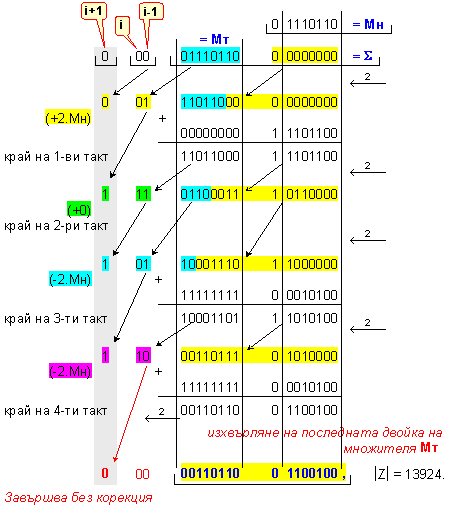
ПРИМЕР 70. Да се изпълни операция умножение Z=X.Y на числата X=118 и Y=118, които са представени в разрядна мрежа с дължина n=8[b], по метода със старшите разряди напред, на два разряда едновременно.

Мн = |X| = 0 1110110 ; Мт = |Y| = 0 1110110.

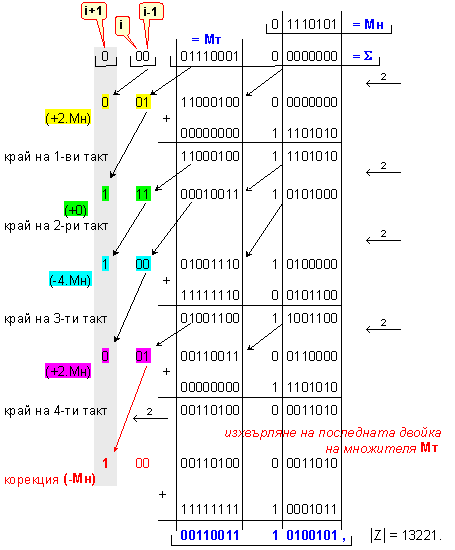
ПРИМЕР 71. Да се изпълни операция умножение Z=X.Y на числата X=117 и Y=113, които са представени в разрядна мрежа с дължина n=8[b], по метода със старшите разряди напред, на два разряда едновременно.

Мн = |X| = 0 1110101 ; Мт = |Y| = 0 1110001.

В) УМНОЖЕНИЕ ПО МОДУЛ С МЛАДШИТЕ РАЗРЯДИ НАПРЕД, ПО СХЕМАТА С НЕПОДВИЖНО МНОЖИМО В ДОПЪЛНИТЕЛЕН КОД

Умножението на числа, представени в допълнителен код, на два разряда едновременно се извършва по алгоритъм, който в последния такт следва да отчете знака на множителя. Известно е, че при отрицателен множител полученото произведение трябва да се коригира. Необходимите за целта операции в последния такт са представени в таблица IV.3.

Таблица IV.3

	Знак на Мт		Операция
0	1	0	- 2.Мн
0	1	1	- Мн
1	1	0	- Мн
1	1	1	+ 0

Както се вижда от таблицата, последната (най-старшата) двойка разряди се формира от знака на множителя и неговата цифра в разряд № (n-2).

Назначената операция е резултат от операциите, определени от цифрата (y_n-2), от стойността на функцията на корекцията и от знака на множителя.

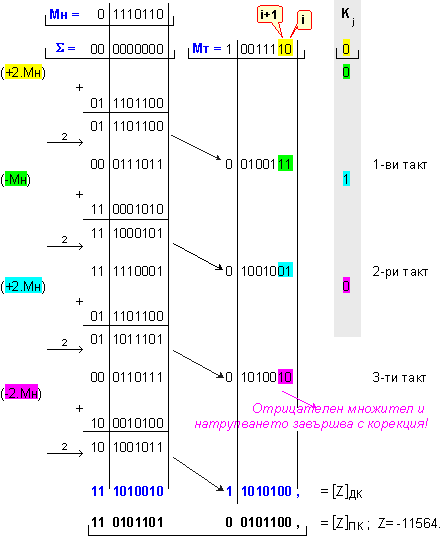
ПРИМЕР 72. Да се изпълни операция умножение Z=X.Y на числата X=118 и Y=-98, които са представени в разрядна мрежа с дължина n=8[b], по метода с два разряда едновременно.

ПРИМЕР 73. Да се изпълни операция умножение Z=X.Y на числата X=-98 и Y=-97, които са представени в разрядна мрежа с дължина n=8[b].

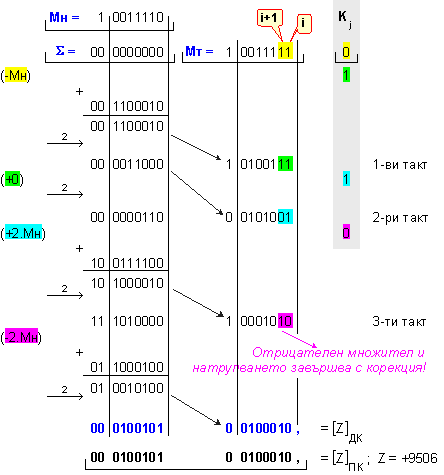
Представените два примера илюстрират само първата комбинация от таблица IV.3, според която в последния такт се назначава операция +2Мн. В следващите примери илюстрираме останалите случаи.

ПРИМЕР 74. Да се изпълни операция умножение Z=X.Y на числата X=-26 и Y=-3.

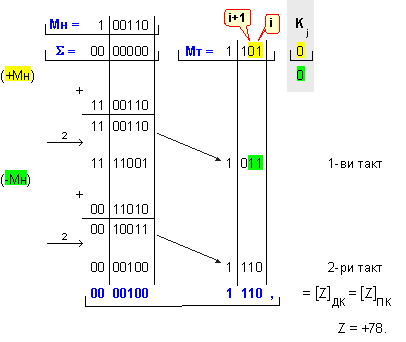
Според получената комбинация (0 11) този пример илюстрира втората комбинация от таблица IV.3, т.е. последната операция е (-Мн).

ПРИМЕР 75. Да се изпълни операция умножение Z=X.Y на числата X=-26 и Y=-5.

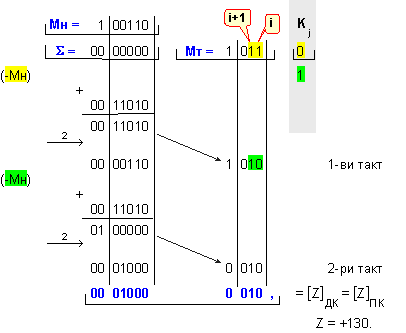
Според получената комбинация (1 10) този пример илюстрира третата комбинация от таблица IV.3, т.е. последната операция е (-Мн).

ПРИМЕР 76. Да се изпълни операция умножение Z=X.Y на числата X=-26 и Y=-1.

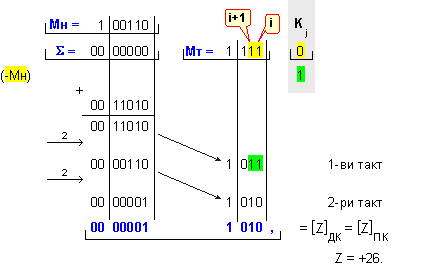
Според получената комбинация (1 11) този пример илюстрира четвъртата комбинация от таблица IV.3, т.е. последната операция е (+0).

Следващият раздел е:

4.3.7 Умножение на числа с ляво фиксирана запетая