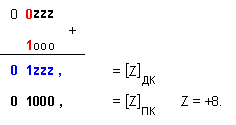Последната редакция на тази книга е от 2021 година.

IV.4.3 Деление на числа със знак в допълнителен код

Общата организация на алгоритъма за деление когато операндите са числа със знак, представени в допълнителен код, е аналогична на вече представената. Разликата, която все пак съществува, се дължи на факта, че тук се отчитат знаците. Те се отчитат в следните моменти:

· При нормализация на операндите;

· При определяне на поредната цифра на частното;

· При определяне на следващата операция.

Характерно за алгоритъма е още това, че в някои от случаите резултатът (т.е. частното) е неточен и се налага да бъде коригиран. Необходимите микрооперации за изпълнение на всеки такт са определени в таблица IV.5, а в таблица IV.6 е представена корекцията на частното при завършване на делението.

Таблица IV.5 Таблица IV.6

Знак на Ост.	Знак на Дт.	Цифра zi	Операция	Знак на Дм.	Знак на Дт.	Корекция на частното в зависимост от последния Остатък
+	+	1	- Дт	+	+	Няма корекция
+	-	0	+ Дт	+	-	+1 винаги
-	+	0	+ Дт	-	+	+1, ако Остатък ¹ 0
-	-	1	- Дт	-	-	+1, ако Остатък = 0

ПРИМЕР 86. Да се изпълни операция деление Z=X/Y на числата X=117 и Y=-6, които са представени в разрядна мрежа с дължина n=10[b] в допълнителен код.

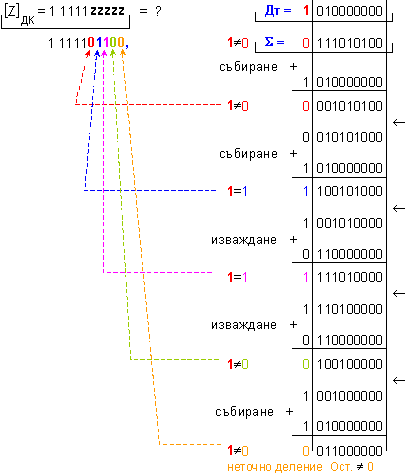
N = 6 - 2 + 1 = 5 (5 неизвестни цифри на частното).

Необходима е корекция +1, според таблица IV.6:

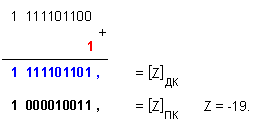
ПРИМЕР 87. Да се изпълни операция деление Z=X/Y на числата X=-512 и Y=-8, които са представени в разрядна мрежа с дължина n=10[b] в допълнителен код.

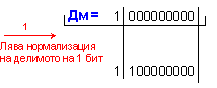
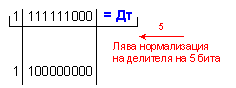
Нормализацията на делимото в този случай се постига чрез изместване надясно на един разряд, тъй като числото е минималното за дадената разрядна мрежа. Тъй като изместването е в обратна посака, противна на типичната, отброяването му в долната формула е със знак минус.

N = 5 - (-1) + 1 = 7 ( 7 неизвестни цифри на частното).

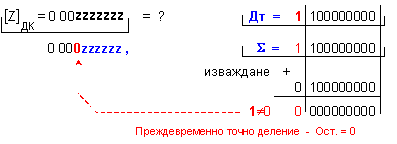
Частното [Z]_ДК = 0 000zzzzzz не е вярно и има още 6 неизвестни цифри !

Според таблица IV.6, в този случай на точно деление, е необходима корекция +1, която се извършва в текущия разряд на частното, след което останалите разряди с още неопределено съдържание се попълват с незначещи цифри, т.е. с нули:

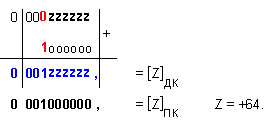
ПРИМЕР 88. Да се изпълни операция деление Z=X/Y на числата X=-117 и Y=-8, които са представени в разрядна мрежа с дължина n=10[b] в допълнителен код.

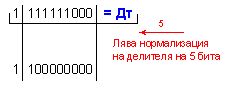
N = 5 - 2 + 1 = 4 (4 неизвестни цифри на частното).

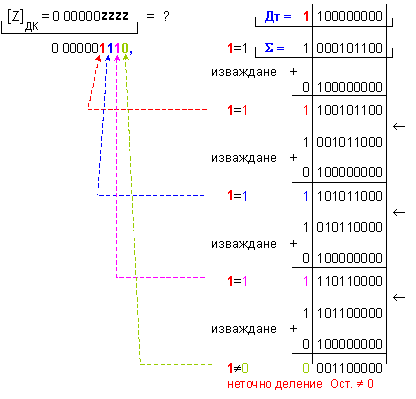
Частното [Z]_ДК = 0 000001110 е вярно, и корекция не е необходима !

ПРИМЕР 89. Да се изпълни операция деление Z=X/Y на числата X=-16 и Y=-1, които са представени в разрядна мрежа с дължина n=5[b] в допълнителен код.

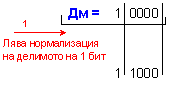
N = 3 - (-1) + 1 = 5.

Тази стойност N=5 е по-голяма от стойността 4=(n-1), която е равна на дължината на цифровата част на дадената разрядна мрежа. Това неравенство N>(n-1) се приема като признак за препълване, тъй като частното (в нашия пример (-16)/(- 1)=+16) е непредставимо в прав код в тази разрядна мрежа.

Независимо каква е дължината на разрядната мрежа, винаги настъпва препълване, ако делимото е равно на минималното представимо число, а делителят е (-1). Това е следствие от несиметричността на диапазона на представимите числа при допълнителен код.

Така този пример следва да завърши без резултат, с генериране на признак за препълване: V=1.

ПРИМЕР 90. Да се изпълни операция деление Z=X/Y на числата X=-8 и Y=-1, които са представени в разрядна мрежа с дължина n=5[b] в допълнителен код.

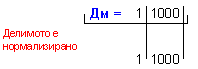
N = 3 - 0 + 1 = 4 (4 неизвестни цифри на частното).

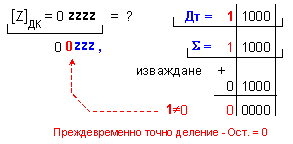
Частното [Z]_ДК = 0 0zzz не е вярно и има още 6 неизвестни цифри !

Според таблица IV.6, в този случай на точно деление, е необходима корекция (+1), която се извършва в текущия разряд на частното, след което останалите разряди с неопределено съдържание се попълват с незначещи цифри, т.е. с нули.

Следващият раздел е:

4.4.3.1 Определяне на остатъка при целочислено деление