IV.4.3.1 Определяне на остатъка при целочислено деление
Вече
многократно,
във връзка с
обяснения, имащи
отношение
към операция
деление Z=X/Y, показахме,
че като
най-сложна,
тази
операция, за
разлика от
всички други,
генерира два
самостоятелни
резултата,
имащи
отношение
към
разнообразни
изисквания в
изчислителните
алгоритми.
Тези два резултата
са частното Z и остатъкът
R.
Тези два
резултата
могат да се
използват в
следното
определение
на операция
деление: Z.Y+R=X.
Ще
припомним
още, че
![]()
при
което Y се нарича модул
за
сравнение
на числото X с
други числа,
които имат
същия
остатък R, както
и още, че
частното Z, в
тази
постановка,
се определя
като коефициент
на кратност
на модула. Точно
в тази
интерпретация,
числото X
може да се
изрази чрез
коефициента
за кратност Z, модула
за сравнение
Y и остатъка,
или още изображението
R, така
X=Z.Y+R.
В
глава 3 на книга
[1] читателят
може да се
запознае с
определящите
операция
деление
алгоритми,
след
прилагането
на които се
получава най-често
търсеният
резултат, а
именно частното.
Машинните
команди на
цифровите
процесори
обаче, както
и тяхната
апаратна
обезпеченост,
са създадени
така, щото те
изчисляват
винаги и
двата
резултата
независимо от
желанията на
потребителя.
Двете числа
остават на
негово
разположение
в два
различни регистъра
в АЛУ.
Читателят
вероятно
вече разбира,
че ние не можем
да оставим
без числена
илюстрация резултата,
за който тук
говорим, ето
защо този
раздел е
посветен на
него. По-долу
са
представени
няколко
числени примера,
които
авторът
счита за
достатъчни при
усвояване на
този проблем.
Теоретично, определянето
на остатъка,
е изложено в раздел 3.2.6
от книга [1]. За
да положим
връзка на
теорията с
практиката,
тук по-долу
ще припомним
част от
теоретичните
зависимости.
Освен това,
за разбиране
на
написаното
по-долу,
авторът
предполага,
че читателят
владее
съответните
алгоритми за
деление, както
и
терминологията,
свързана с
тях.
И така, след съответни замествания в лявата част на равенството (3.2.6.10.а) (вижте в книга [1]), се стига до следното равенство
![]()
Горното равенство е забележително с това, че то изразява как може да се получи вторият резултат от операция деление, а именно остатъкът Rx от делението. Изводът е, че остатъкът Rx се съдържа в последния частичен остатък Rk-l+1, който следва да се измести на (k-l) бита надясно, за да се представи правилно като цяло число. Това число е със знак и ще бъде получено автоматично в допълнителен код.
Необходимо
е още едно
пояснение.
Ако
последното
изваждане,
при което се
получава
последният
частичен
остатък Rk-l+1, е било
успешно, то
той съдържа
търсения остатък
Rx. Ако обаче
изваждането
не е било
успешно, то
от последния
частичен
остатък Rk-l+1
следва да се
възстанови
предидущия
частичен
остатък, в
който трябва
да се съдържа
търсения
остатък Rx. В крайна
сметка, както
читателят ще
може да се
увери от
представените
по-долу
числени
примери, може
да
формулираме
следното кратко
правило:
А)
ДЕЛЕНИЕ ПО МОДУЛ
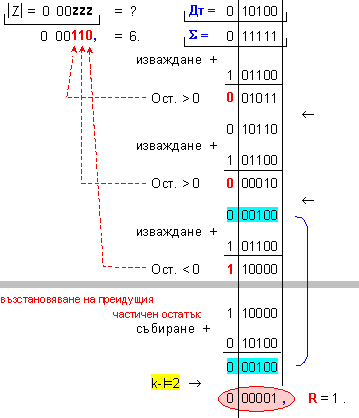
ПРИМЕР 91. Да се
изпълни
операция
деление Z=X/Y на
числата X=31 и
Y=5, които
са
представени
в разрядна мрежа
с дължина n=6[b]
. Следва да
получим този
отговор:
частно Z=6 и
остатък R=1, т.е. 31=6.5+1 .
Дм
= |X| =
0 11111 ; Дт = |Y| = 0 00101
.


N = 2 - 0 + 1 = 3
( 3
неизвестни
цифри на
частното )
k-l = 2-0 = 2
-
изместване
на 2[b] за
формиране на
остатъка.
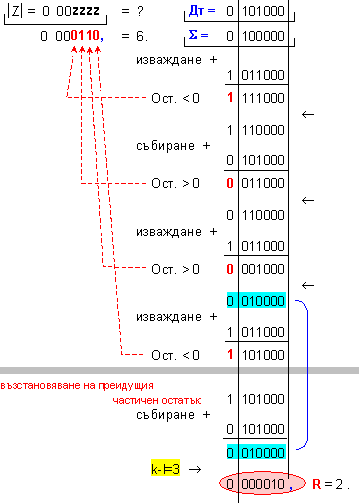
ПРИМЕР 92. Да се
изпълни
операция
деление Z=X/Y на
числата X=32 и
Y=5, които
са
представени
в разрядна мрежа
с дължина n=7[b]
. Следва да получим
този отговор:
частно Z=6 и
остатък R=2, т.е. 32=6.5+2 .
Дм
= |X| =
0 100000 ; Дт = |Y| = 0 000101
.


N = 3 - 0 + 1 = 4
( 4
неизвестни
цифри на частното
)
k-l = 3-0 = 3
-
изместванe
на 3[b] за
формиране на
остатъка.
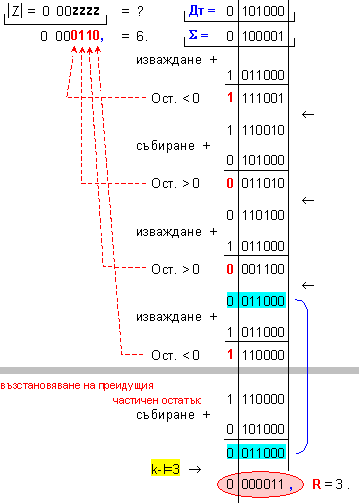
ПРИМЕР 93. Да се
изпълни
операция
деление Z=X/Y на
числата X=33 и
Y=5, които
са
представени
в разрядна мрежа
с дължина n=7[b]
. Следва да получим
този отговор:
частно Z=6 и
остатък R=3, т.е. 33=6.5+3 .
Дм
= |X| =
0 100001 ; Дт = |Y| = 0 000101
.


N = 3 - 0 + 1 = 4
( 4
неизвестни
цифри на частното
)
k-l = 3-0 = 3
-
изместванe
на 3[b] за
формиране на
остатъка.
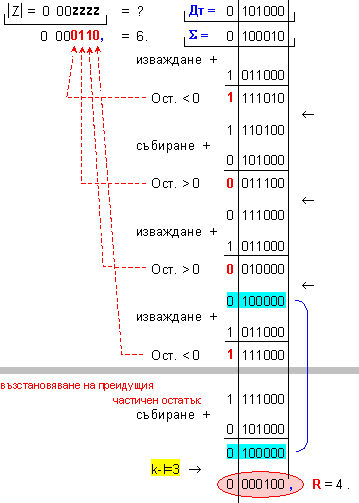
ПРИМЕР 94. Да се
изпълни
операция
деление Z=X/Y на
числата X=34 и
Y=5, които
са
представени
в разрядна мрежа
с дължина n=7[b]
. Следва да
получим този
отговор:
частно Z=6 и
остатък R=4, т.е. 34=6.5+4 .
Дм
= |X| =
0 100010 ; Дт = |Y| = 0 000101
.


N = 3 - 0 + 1 = 4
( 4
неизвестни
цифри на частното
)
k-l = 3-0 = 3
-
изместванe
на 3[b] за
формиране на
остатъка.
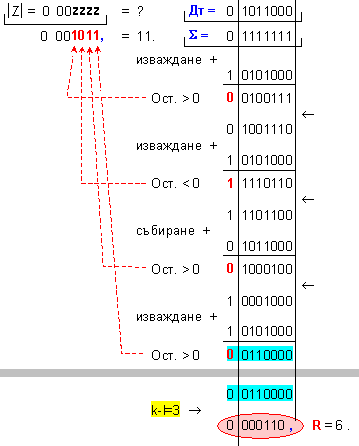
ПРИМЕР 95. Да се
изпълни
операция
деление Z=X/Y на
числата X=127 и
Y=11, които
са
представени
в разрядна мрежа
с дължина n=8[b]
. Следва да получим
този отговор:
частно Z=11 и
остатък R=6, т.е. 127=11.11+6 .
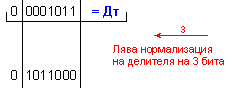
Дм
= |X| =
0 1111111 ; Дт = |Y| = 0 0001011
.
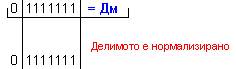
N = 3 - 0 + 1 = 4
( 4
неизвестни
цифри на
частното )
k-l = 3-0 = 3
-
изместванe
на 3[b] за
формиране на
остатъка.
ПРИМЕР 96. Да се
изпълни
операция
деление Z=X/Y на
числата X=126 и
Y=11, които
са
представени
в разрядна мрежа
с дължина n=8[b]
. Следва да
получим този
отговор:
частно Z=11 и
остатък R=5, т.е. 126=11.11+5 .
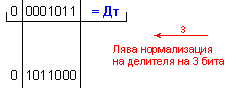
Дм
= |X| =
0 1111110 ; Дт = |Y| = 0 0001011
.
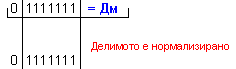
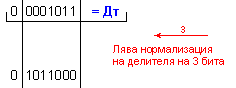
N = 3 - 0 + 1 = 4
( 4 неизвестни
цифри на
частното )
k-l = 3-0 = 3
-
изместванe
на 3[b] за
формиране на
остатъка.
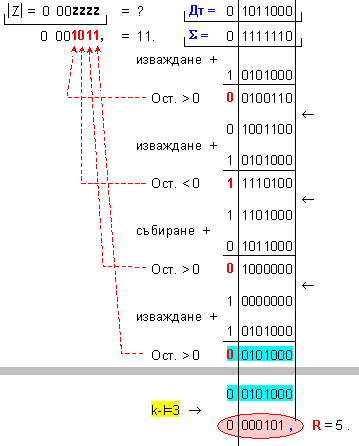
ПРИМЕР 97. Да се
изпълни
операция
деление Z=X/Y на
числата X=125 и
Y=11, които
са
представени
в разрядна мрежа
с дължина n=8[b]
. Следва да
получим този
отговор:
частно Z=11 и остатък R=4,
т.е. 125=11.11+4 .
Дм
= |X| =
0 1111101 ; Дт = |Y| = 0 0001011
.
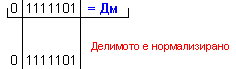
N = 3 - 0 + 1 = 4
( 4 неизвестни
цифри на
частното )
k-l = 3-0 = 3
-
изместванe
на 3[b] за
формиране на
остатъка.
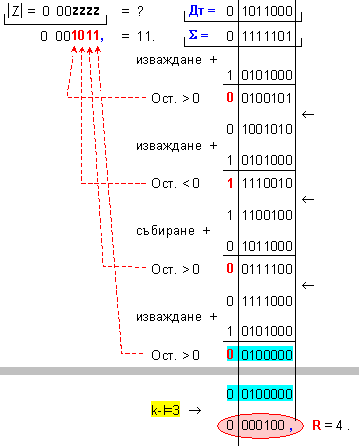
ПРИМЕР 98. Да се
изпълни
операция
деление Z=X/Y на
числата X=120 и
Y=11, които
са
представени
в разрядна мрежа
с дължина n=8[b]
. Следва да
получим този
отговор:
частно Z=10 и остатък R=10,
т.е. 120=10.11+10 .
Дм
= |X| =
0 1111000 ; Дт = |Y| = 0 0001011
.
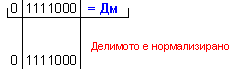
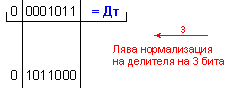
N = 3 - 0 + 1 = 4
( 4
неизвестни
цифри на
частното )
k-l = 3-0 = 3
-
изместванe
на 3[b] за
формиране на
остатъка.
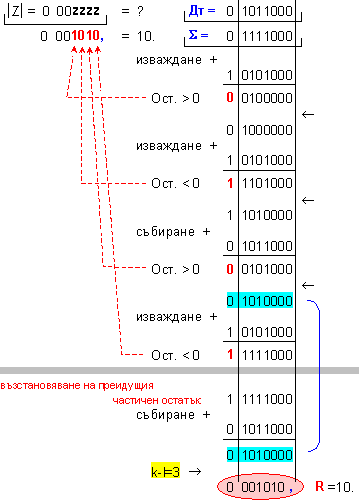
ПРИМЕР 99. Да се
изпълни
операция
деление Z=X/Y на
числата X=119 и
Y=11, които
са
представени
в разрядна мрежа
с дължина n=8[b]
. Следва да
получим този
отговор:
частно Z=10 и остатък R=9,
т.е. 119=10.11+9 .
Дм
= |X| =
0 1110111 ; Дт = |Y| = 0 0001011
.
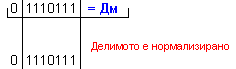
N = 3 - 0 + 1 = 4
( 4
неизвестни
цифри на
частното )
k-l = 3-0 = 3
-
изместванe
на 3[b] за
формиране на
остатъка.
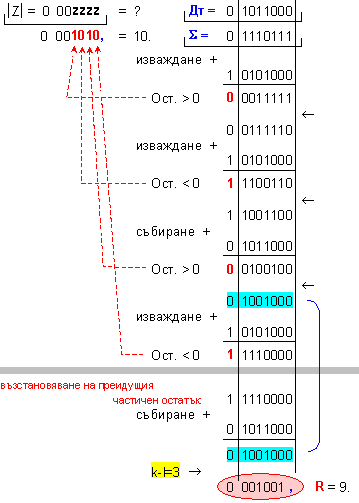
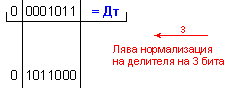
ПРИМЕР 100. Да се
изпълни
операция
деление Z=X/Y на
числата X=119 и
Y=10, които
са
представени
в разрядна мрежа
с дължина n=8[b]
. Следва да
получим този
отговор:
частно Z=11 и остатък R=9,
т.е. 119=11.10+9 .
Дм
= |X| =
0 1110111 ; Дт = |Y| = 0 0001010
.
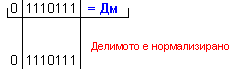
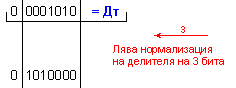
N = 3 - 0 + 1 = 4
( 4
неизвестни
цифри на
частното )
k-l = 3-0 = 3
-
изместванe
на 3[b] за
формиране на
остатъка.
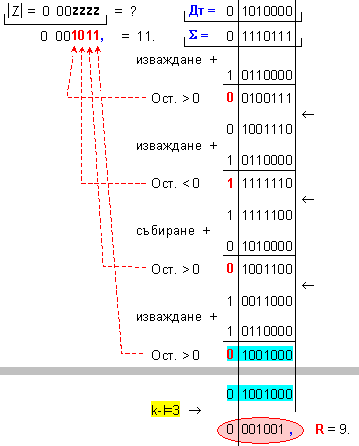
ПРИМЕР 101. Да се
изпълни
операция
деление Z=X/Y на
числата X=119 и
Y=5, които
са
представени
в разрядна
мрежа с
дължина n=8[b] .
Следва да
получим този
отговор:
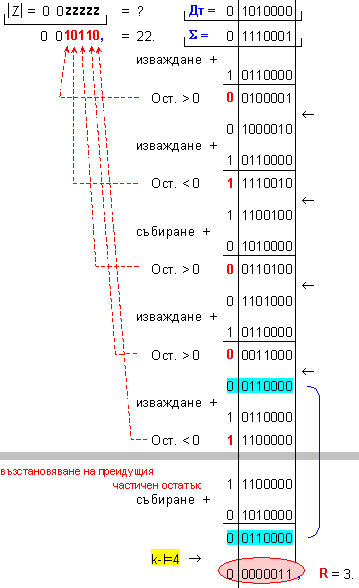
частно Z=23 и остатък R=4,
т.е. 119=23.5+4 .
Дм
= |X| =
0 1110111 ; Дт = |Y| = 0 0000101
.
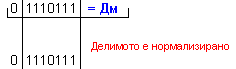
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
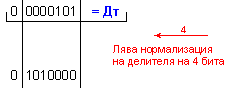
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
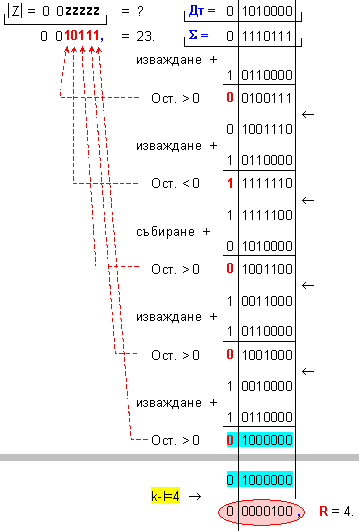
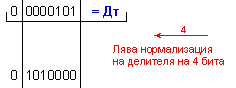
ПРИМЕР 102. Да се
изпълни
операция
деление Z=X/Y на
числата X=113 и
Y=5, които
са
представени
в разрядна
мрежа с
дължина n=8[b] .
Следва да
получим този
отговор:
частно Z=22 и остатък R=3,
т.е. 113=22.5+3 .
Дм
= |X| =
0 1110001 ; Дт = |Y| = 0 0000101
.
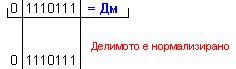
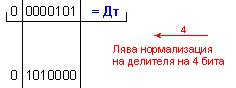
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
Б)
ДЕЛЕНИЕ НА ЧИСЛА,
ПРЕДСТАВЕНИ В
ДОПЪЛНИТЕЛЕН КОД
При деление на числа в допълнителен код на всеки такт трябва да се определя поредната цифра, която се записва в частното, както и да се определя следващата операция. Освен това в края на делението трябва да се извършва проверка за необходимост от корекция на частното. Ако такава е необходима, то в края на делението, към частното се прибавя единица. Тъй като числата със знак, остатъкът носи знака на делимото, но само ако частното е отрицателно (т.е. операндите са с различни знаци). Остатъкът се получава в допълнителен код.
ПРИМЕР 103. Да се
изпълни
операция
деление Z=X/Y на
числата X=113 и
Y=-5, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=-22 и
остатък R=+3, т.е. 113=(-22).(-5)+3 .
![]()
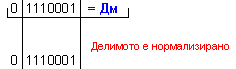
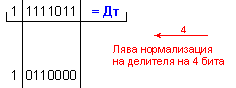
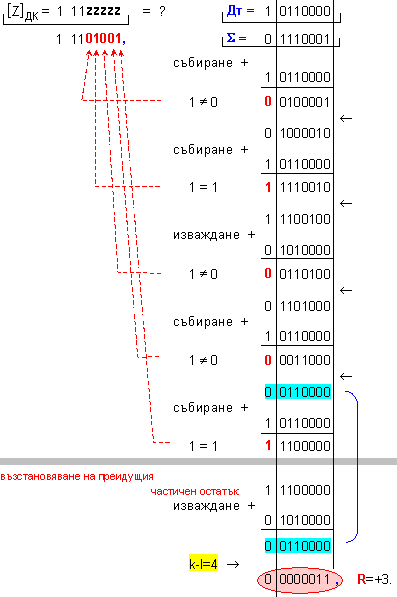
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
Корекция на частното:
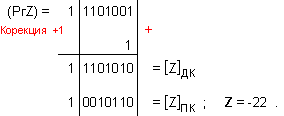
ПРИМЕР 104. Да се
изпълни
операция
деление Z=X/Y на
числата X=-113 и
Y=5, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=-22 и
остатък R=-3, т.е. (-113)=(-22).(5)-3 .
![]()
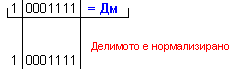
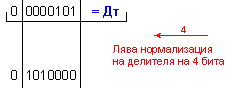
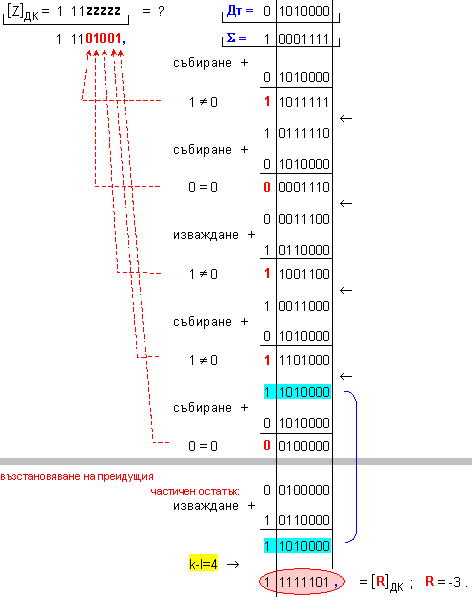
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
Корекция на частното:
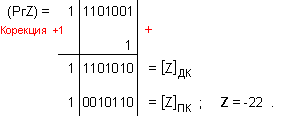
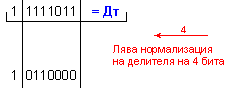
ПРИМЕР 105. Да се
изпълни
операция
деление Z=X/Y на
числата X=-113 и
Y=-5, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=22 и
остатък R=-3, т.е. (-113)=22.(-5)-3 .
![]()
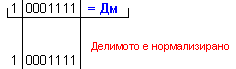
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
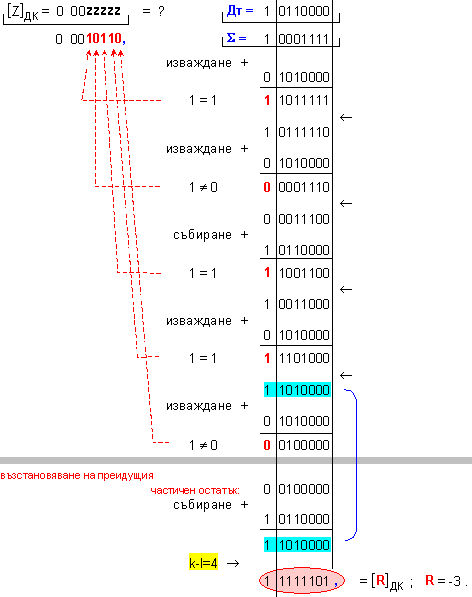
Корекция
на частното:
в този
случай
частното не
се нуждае от
корекция, Z=22.
ПРИМЕР 106. Да се
изпълни
операция
деление Z=X/Y на
числата X=+119 и
Y=+5, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+23 и
остатък R=+4, т.е. 119=23.5+4 .
![]()
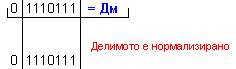
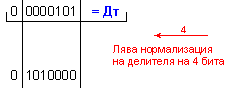
N = 4 - 0 + 1 = 5
( 5 неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
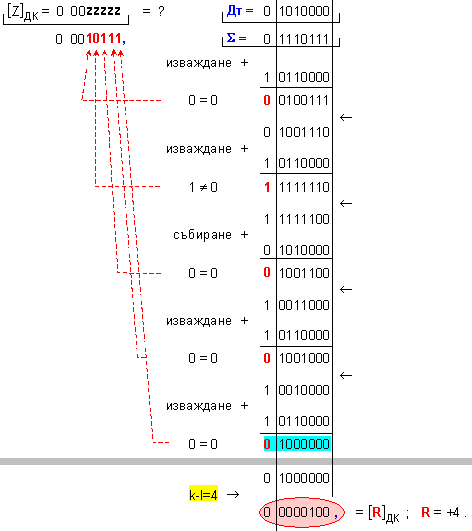
Корекция
на частното:
в този
случай
частното не
се нуждае от
корекция, Z=+23.
ПРИМЕР 107. Да се
изпълни
операция
деление Z=X/Y на
числата X=+119 и
Y=-5, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=-23 и
остатък R=+4, т.е. 119=(-23).(-5)+4 .
![]()
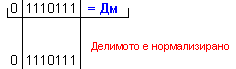
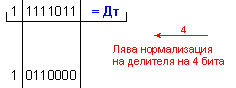
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
Корекция на частното:
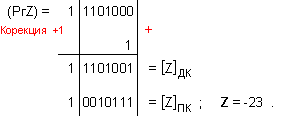
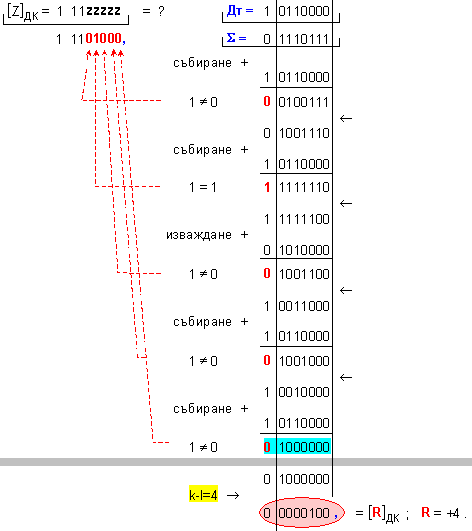
ПРИМЕР 108. Да се
изпълни
операция
деление Z=X/Y на
числата X=-119 и
Y=+5, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=-23 и
остатък R=-4, т.е. (-119)=(-23).(+5)-4 .
![]()
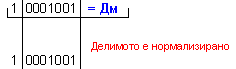
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
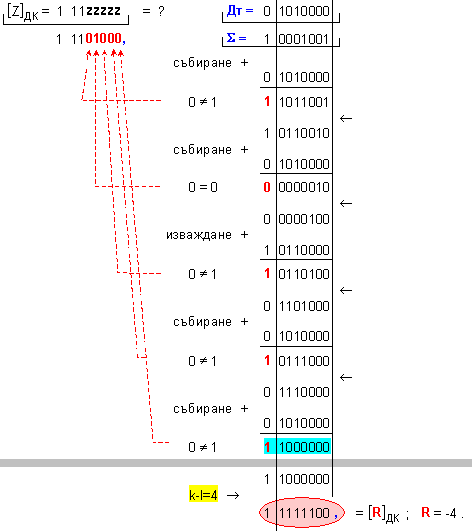
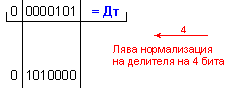
Корекция на частното:
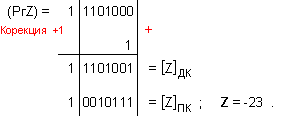
ПРИМЕР 109. Да се
изпълни
операция
деление Z=X/Y на
числата X=-115 и
Y=+5, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=-23 и
остатък R=0, т.е. (-115)=(-23).(+5)+0 .
![]()
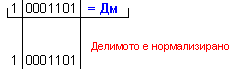
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
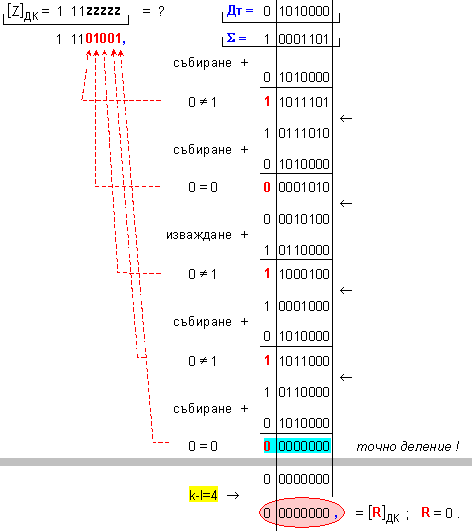
Корекция
на частното:
в този
случай
частното не
се нуждае от
корекция [Z]ДК = 1 1101001
, чийто прав
код е [Z]ПК = 1
0010111 ,
което е Z = -23 .
ПРИМЕР 110. Да се
изпълни
операция
деление Z=X/Y на
числата X=-115 и
Y=-5, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+23 и
остатък R=0, т.е. (-115)=(23).(-5)+0 .
![]()
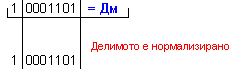
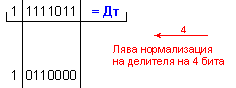
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
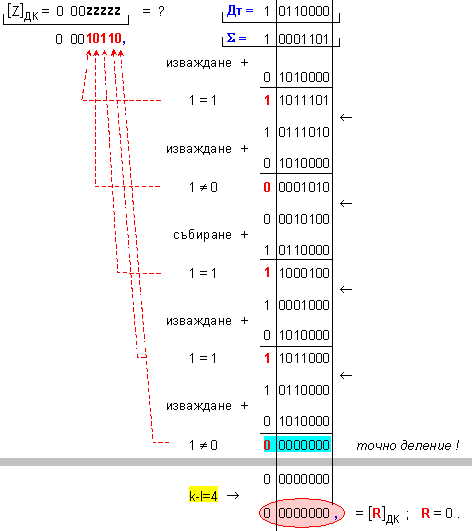
Корекция
на частното:
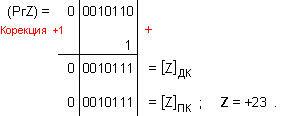
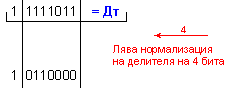
ПРИМЕР 111. Да се
изпълни операция
деление Z=X/Y на
числата X=-116 и
Y=-5, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+23 и
остатък R=-1, т.е. (-116)=(23).(-5)-1 .
![]()
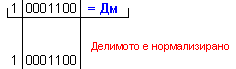
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
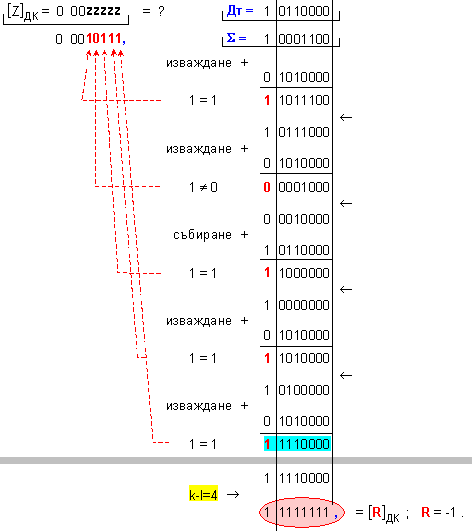
Корекция
на частното: в този
случай частното
не се нуждае
от корекция Z=+23 .
ПРИМЕР 112. Да се
изпълни
операция
деление Z=X/Y на
числата X=-131 и
Y=-5, които
са
представени
в разрядна мрежа
с дължина n=9[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+26 и
остатък R=-1, т.е. (-131)=(26).(-5)-1 .
![]()


N = 5 - 0 + 1 = 6
( 6
неизвестни
цифри на
частното )
k-l = 5-0 = 5
-
изместванe
на 5[b] за
формиране на
остатъка.
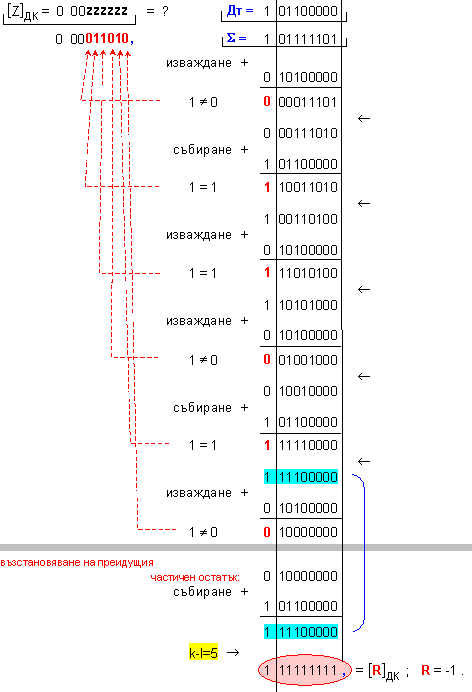
Корекция
на частното: в този
случай
частното не
се нуждае от
корекция Z=+26 .
ПРИМЕР 113. Да се
изпълни
операция
деление Z=X/Y на
числата X=-238 и
Y=-14, които
са
представени
в разрядна мрежа
с дължина n=9[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+17 и
остатък R=0, т.е. (-238)=(+17).(-14)+0 .
![]()

N = 4 - 0 + 1 = 5
( 5
неизвестни цифри
на частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
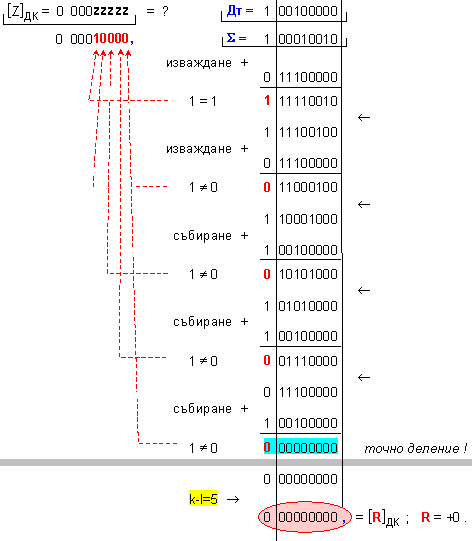
Корекция
на частното:
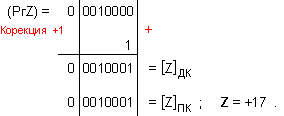
ПРИМЕР 114. Да се
изпълни
операция
деление Z=X/Y на
числата X=+97 и
Y=+7, които са
представени
в разрядна
мрежа с
дължина n=8[b] в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+13 и
остатък R=+6, т.е. 97=13.7+6 .
![]()
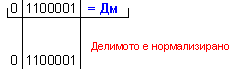
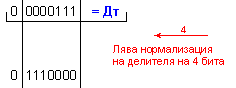
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
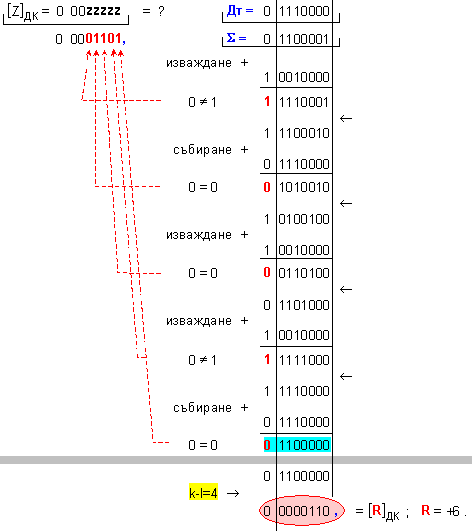
Корекция
на частното: в този
случай
частното не
се нуждае от
корекция Z=+13 .
ПРИМЕР 115. Да се
изпълни
операция
деление Z=X/Y на
числата X=+97 и
Y=-7, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=-13 и
остатък R=+6, т.е. 97=13.7+6 .
![]()
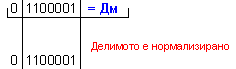
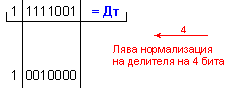
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
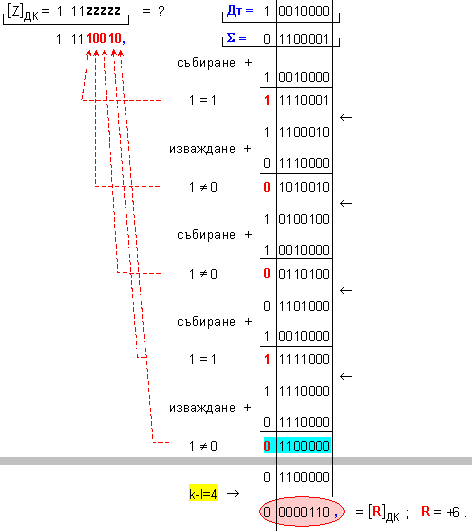
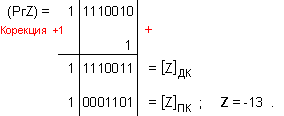
ПРИМЕР 116. Да се
изпълни
операция
деление Z=X/Y на
числата X=-97 и
Y=+7, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=-13 и
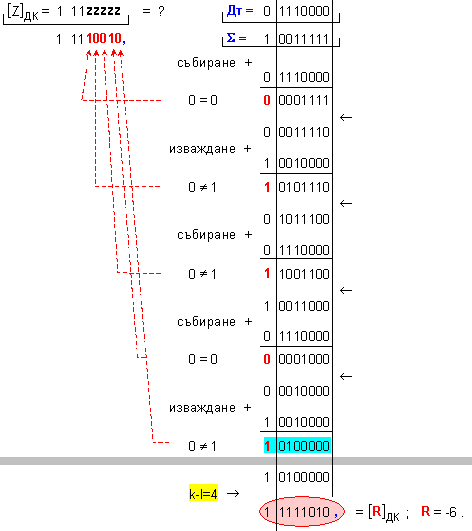
остатък R=-6, т.е. (-97)=(-13).7-6 .
![]()
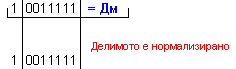
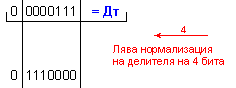
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
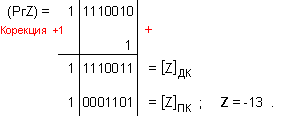
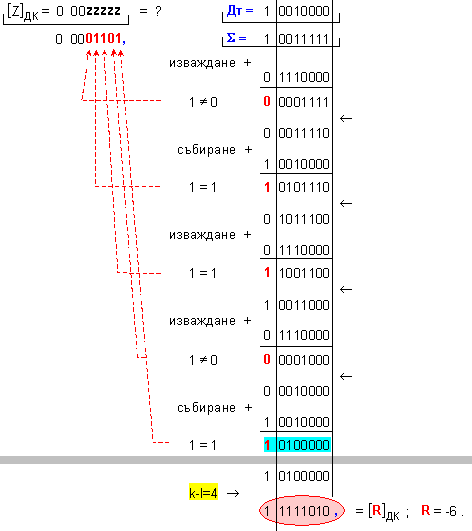
ПРИМЕР 117. Да се
изпълни
операция
деление Z=X/Y на
числата X=-97 и
Y=-7, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+13 и остатък R=-6,
т.е. (-97)=13.(-7)-6
.
![]()
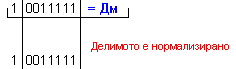
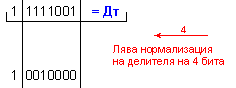
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
ПРИМЕР 118. Да се
изпълни
операция
деление Z=X/Y на
числата X=+100 и
Y=+7, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+14 и
остатък R=+2, т.е. 100=14.7+2 .
![]()
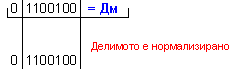
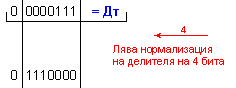
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на частното
)
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
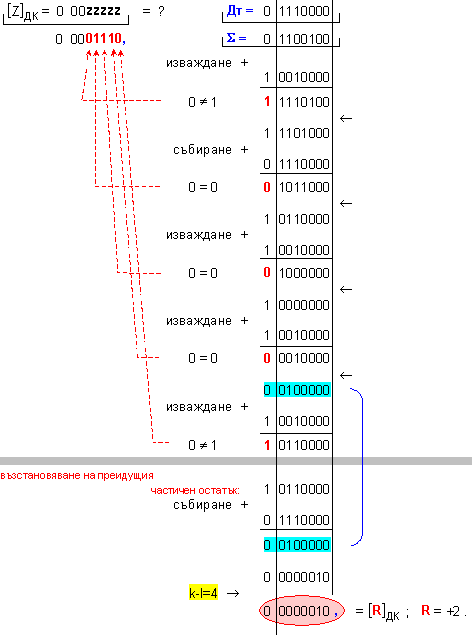
Корекция
на частното: в този
случай
частното не
се нуждае от
корекция Z=+14 .
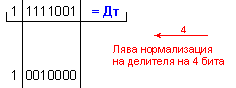
ПРИМЕР 119. Да се
изпълни
операция
деление Z=X/Y на
числата X=+100 и
Y=-7, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=-14 и
остатък R=+2, т.е. 100=(-14).(-7)+2 .
![]()
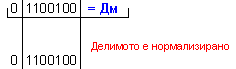
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
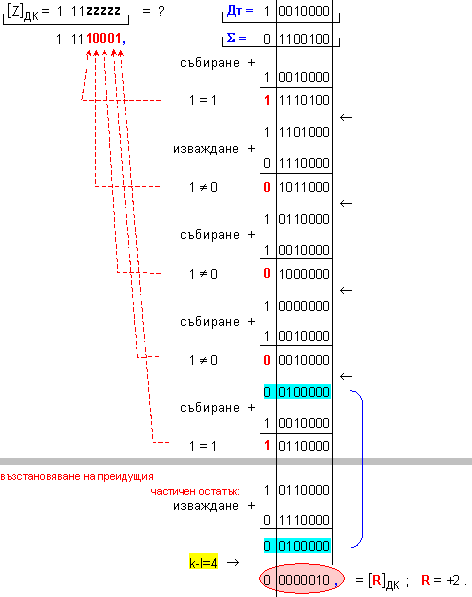
Корекция
на частното:
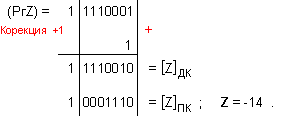
ПРИМЕР 120. Да се
изпълни
операция
деление Z=X/Y на
числата X=-100 и
Y=+7, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
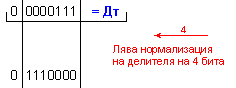
частно Z=-14 и
остатък R=-2, т.е. (-100)=(-14).7-2 .
![]()
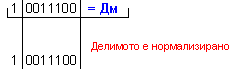
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
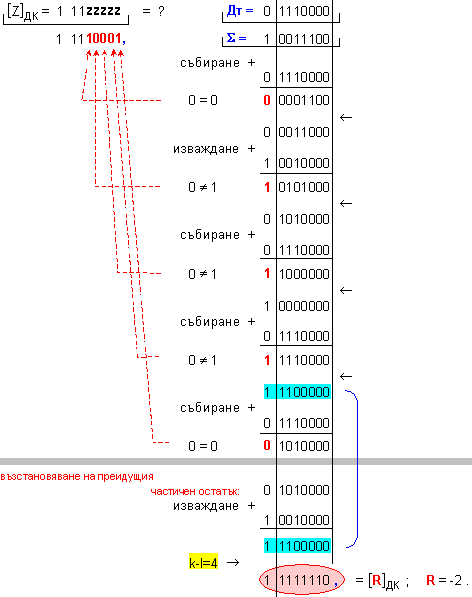
Корекция
на частното:
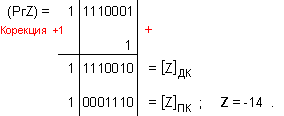
ПРИМЕР 121. Да се
изпълни
операция
деление Z=X/Y на
числата X=-100 и
Y=-7, които
са
представени
в разрядна мрежа
с дължина n=8[b]
в
допълнителен
код. Следва
да получим
този отговор:
частно Z=+14 и
остатък R=-2, т.е. (-100)=14.(-7)-2 .
![]()
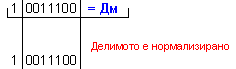
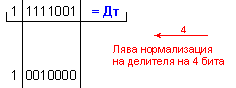
N = 4 - 0 + 1 = 5
( 5
неизвестни
цифри на
частното )
k-l = 4-0 = 4
-
изместванe
на 4[b] за
формиране на
остатъка.
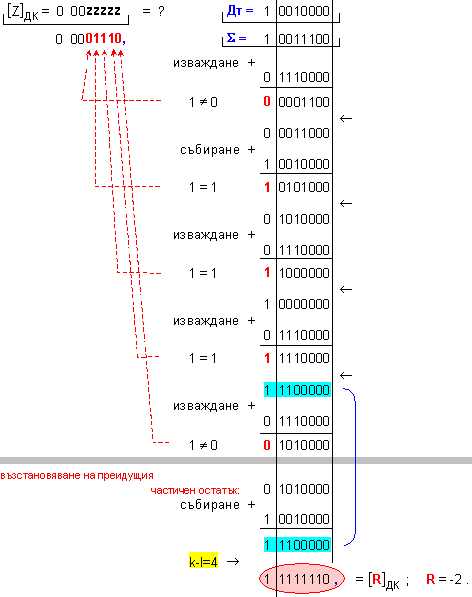
Корекция
на частното: в този
случай
частното не
се нуждае от
корекция Z=+14 .