Последната редакция на тази книга е от 2021 година.

IV.4.4 Деление на числа с ляво фиксирана запетая в допълнителен код

Тук има смисъл да се демонстрира алгоритъмът за деление при предварителното условие, че операндите с ляво фиксирана запетая, са ляво нормализирани числа. Това условие произтича от факта, че числата с ляво фиксирана запетая представляват мантиси във формата с плаваща запетая. В тази връзка следва още да припомним, че мантисите на числата с плаваща запетая се представят в прав код. Все пак числената илюстрация тук ще бъде върху числа, чийто знак се отчита, т.е. те са представени в допълнителен код.

Както и в предидущите алгоритми, делението започва с необходимите проверки на условията за дефинираност и изпълнимост на операцията. За да не настъпва препълване е необходимо изпълнение на неравенството

|Дм| < |Дт| .

В този случай всичките n разряда на частното са неизвестни. Горното условие обаче не винаги е изпълнено, модулът на мантисата на делимото може да е по-голяма или равна на модула на мантисата на делителя. Тогава частното ще се намира в диапазона

[ -(2-2^(-n)) ¸ +(2-2^(-n)) ]

ПРИМЕР 126. Да се изпълни операция деление Z=X/Y на числата X=0,53125 и Y=-0,875 , които са представени в разрядна мрежа с дължина n=6[b] в допълнителен код.

Този резултат:

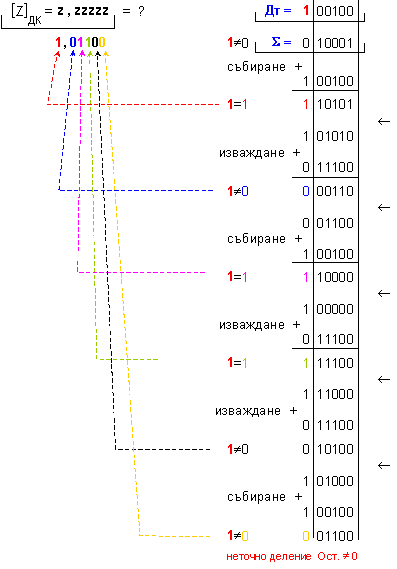
не е верен, необходима е корекция:

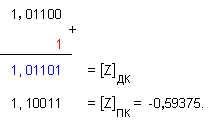
Получените 5 двоични цифри в дробната част на частното са недостатъчни за приближаване на резултата до точната му стойност, изчислена в началото на примера. За постигане на по-висока точност, процесът на деление може да бъде продължен, като частното се получи в удължен формат, както е показано по-надолу с продължението на примера:

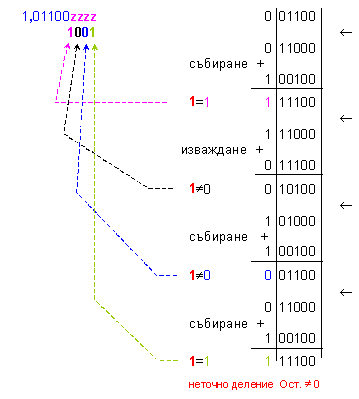
Този нов резултат:

също не е верен, необходима е корекция:

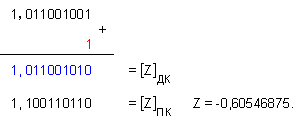
Този резултат отново е неточен, но е значително по-близък до истинския !

Следващият раздел е:

4.4.5 Деление по алгоритъма на малките остатъци