IV.5 Събиране и изваждане на двоично-десетични числа
Кодирането
на 2/10-ните
числа, както
и апаратната
реализация
на операция
събиране
беше представена
в раздел III на тази
книга. Тук
ще се
разгледат
операциите
върху 2/10-ните
числа със
знак. За целта
ще се
използуват
инверсните
машинни
кодове
(обратен,
допълнителен)
при представяне
на числата.
А) Числа,
кодирани в
код 8421.
Обратният
код на всяка i-та
цифра на едно
отрицателно
число X се
определя
както следва:
![]()
а
допълнителният
код на цялото
число така:
![]()
Обратният
и
допълнителният
кодове на едно
положително
число X
съвпадат с
правия му
код.
Б) Числа,
кодирани в
код с излишък
+3.
Обратният
код на всяка i-та
цифра на едно
отрицателно
число X се
определя
както следва:
![]()
а
допълнителният
код на цялото
число така:
![]()
Обратният
и
допълнителният
кодове на едно
положително
число X
съвпадат с
правия му
код.
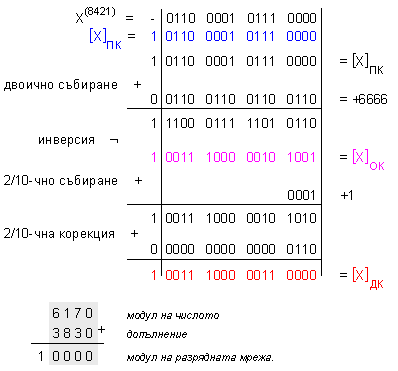
ПРИМЕР 131.
Да се
представи 2/10-ното
число X(8421) = -6170 в прав,
обратен и
допълнителен
код в 4
разрядна
мрежа.
ПРИМЕР 132.
Да се
представи 2/10-ното
число X(8421) = -3369 в прав,
обратен и
допълнителен
код в 5
разрядна
мрежа.

ПРИМЕР 133.
Да се
представи 2/10-ното
число
X(+3) = -6170 в прав,
обратен и
допълнителен
код в 4
разрядна
мрежа.
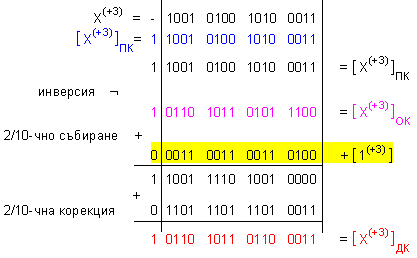
ПРИМЕР 134.
Да се
представи 2/10-ното
число X(+3) = -3369 в
прав, обратен
и допълнителен
код в 5
разрядна
мрежа.
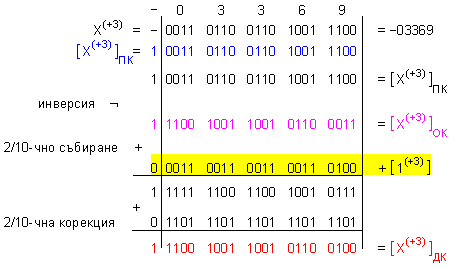
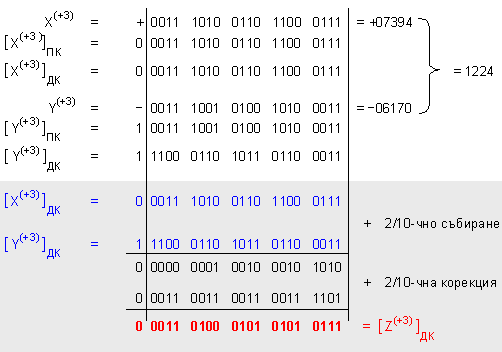
ПРИМЕР 135.
Да се
изпълни
операция
събиране Z=X+Y на
числата X=7394 и Y=-6170, които
са
представени
в разрядна
мрежа с дължина n=5 [2/10-ни
разряда].
А)
събиране
в код (8421)

Б) събиране в
код с излишък
(+3)
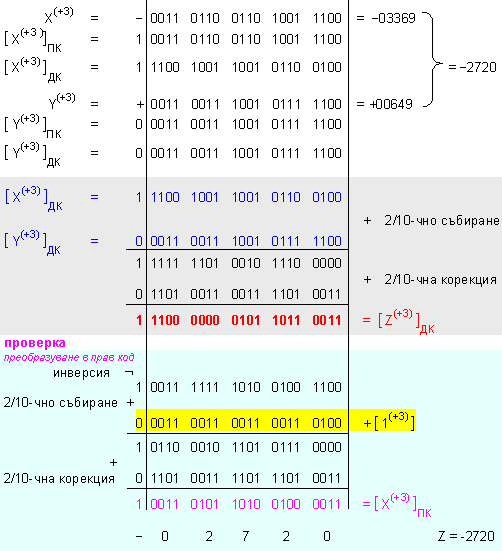
ПРИМЕР 136. Да се
изпълни
операция
събиране Z=X+Y на
числата X=-3369 и Y=0649, които
са
представени
в разрядна
мрежа с дължина n=5 [2/10-ни
разряда].
А)
събиране
в код (8421)

Б) събиране в
код с излишък
(+3)
ПРИМЕР 137. Да се
изпълни
операция
изваждане Z=X-Y на
числата X=6170 и
Y=7856, които са
представени
в разрядна мрежа
с дължина n=5 [2/10-ни
разряда].
А)
изваждане
в код (8421)

Б)
изваждане
в код с
излишък (+3)

Следващият
раздел е:
4.5.1
Събиране и
изваждане на
двоично-десетични
числа в код 2421