IV.5.1 Събиране и изваждане на двоично-десетични числа в код 2421
Същността
на операция
изваждане е
изложена в книга [1] и
нито
бройната
система, нито
кодът, правят
изключение,
ето защо са в
сила приложимостта
на
допълнителния
код и неговите
свойства. Тъй
като за кодът
2421 свойството
допълняемост
е изпълнено,
то може да
бъде
използвано
следното
определение
за получаване
на
допълнителен
код:
![]()
Според
теоремата за
събиране в допълнителен
код,
операциите
събиране и
изваждане се
изпълняват
върху
допълнителните
кодове на
числата.
Според
казаното
по-горе,
допълнителният
код на едно
отрицателно
число в код 2421
се получава
след
поразрядно логическо
инвертиране,
в резултат на
което се
получава
обратният му
код, с
последващо
инкрементиране.
ПРИМЕР 138. Да се
изчисли
сумата
Z=X+Y, където X=3497889,
Y=1434595.
Тогава Z=4932484.


ПРИМЕР 139. Да се
изчисли
разликата Z=X-Y,
където X=3497889, Y=1434595.
Тогава
Z=2063294.
В
този пример
първоначално
ще бъде
получен
допълнителният
код на
числото -Y.
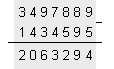

Следва
изпълнение
на операция
събиране в допълнителен
код:

ПРИМЕР 140. Да се
изчисли
разликата Z=Y-X,
където X=3497889, Y=1434595.
Тогава
Z=-2063294.

Ще
получим
допълнителният
код на
числото –Y:
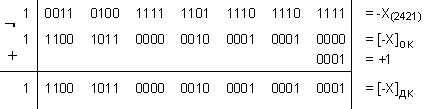
Следва
изпълнение
на операция
събиране в
допълнителен
код:

Тъй като
след
събирането
препълване
няма, то
полученият
резултат е
верен, но е
представен в
допълнителен
код. За да
направим проверка,
трябва да го
преобразуваме
в прав код. За
целта
прилагаме
същия алгоритъм
(за
получаване
на ДК):

Както се
вижда от
получените
резултати, приложената
логика води
до верни
резултати.
4.5.2
Събиране и
изваждане на
двоично-десетични
числа в код 5211