IV.5.2.
Събиране и
изваждане на
двоично-десетични
числа в код 5211
Кодирането
на десетични
цифри е
ключов въпрос
за
осигуряване
на бърза
десетична аритметика.
Последните
разработки
предполагат
използването
на
алтернативни
BCD кодове, като
например BCD-5211,
чрез който
при събиране
се постига
пълна
аналогия с
десетичния
пренос. Кодът
BCD-5211 предоставя
определено
предимство
по отношение
на код BCD-4221 или BCD-8421.
Кодът 5211 е
тегловно
значим (t3t2t1t0)
и е един от 17-те
4-битови BCD-кода
с
положителни
тегла (вижте
книга [1]). Този код
се определя
като
перспективен
за реализация
на десетична
аритметика,
особено за
операции
умножение и
деление. При
операции
събиране и
изваждане,
както ще бъде
показано
по-долу,
кодът
позволява
имитация на
десетичния
пренос
(съответно
заем).
BCD тегловен код 5211
При
кодиране на
десетичните
цифри в код 5211 се
използват
само 10 от
възможните 16
4-битови двоични
комбинации.
Еднозначно
се кодират само
цифрите 0, 4, 5 и 9.
Останалите
шест цифри не
могат да се
кодират
еднозначно.
За всяка от
цифрите 1, 2, 3, 6, 7 и 8
могат да се
формират по
две различни
кодови комбинации,
така че
общият брой
на възможните
кодови
таблици е 26=64.
Този брой е
твърде голям
за да е
възможно изследването
му тук. В
литературните
източници не
се намира
единно
предложение
за избор на
кодова
таблица, като
при своя
избор авторите
обикновено
залагат на
свойството допълняемост
(вижте
свойствата
на Рутизхауер
в книга [1]).
Нашата
проверка на
кодови таблици
с това
свойство
обаче показа,
че то води до
по-сложни
правила за
операция
събиране, ето
защо тук ние
предлагаме
следните две
кодови
таблици:
Кодови
таблици на
2/10-чен
тегловен код
5211
Таблица
1.
Таблица 2.
|
d |
t3 |
t2 |
t1 |
t0 |
|
d |
t3 |
t2 |
t1 |
t0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
2 |
0 |
0 |
1 |
1 |
|
2 |
0 |
0 |
1 |
1 |
|
3 |
0 |
1 |
0 |
1 |
|
3 |
0 |
1 |
0 |
1 |
|
4 |
0 |
1 |
1 |
1 |
|
4 |
0 |
1 |
1 |
1 |
|
5 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
0 |
0 |
|
6 |
1 |
0 |
0 |
1 |
|
6 |
1 |
0 |
1 |
0 |
|
7 |
1 |
0 |
1 |
1 |
|
7 |
1 |
1 |
0 |
0 |
|
8 |
1 |
1 |
0 |
1 |
|
8 |
1 |
1 |
0 |
1 |
|
9 |
1 |
1 |
1 |
1 |
|
9 |
1 |
1 |
1 |
1 |
Правила
за 2/10-чно
събиране в
код 5211
(кодова таблица
1)
Както при
всеки
известен
2/10-чен суматор
(вижте
по-горе в
тази книга
раздел 3) и тук
за операция
събиране се
налага
синтез на
двуетажна
логическа
структура на
суматора в
този код.
Тава се дължи
на различията
между
бройните
системи.
Както на
първия, така
и на втория
суматор се
използват
4-битови
двоични
суматори.
Двоичната сумата
от първия
етаж
![]()
не
винаги е
вярна (в
смисъла на
кодовата таблица).
Във всички
случаи,
когато тя не е
вярна, се
налага
корекция,
стойността
на която се
определя по
силата на
синтезираните
и
представени
по-долу
правила. В
резултат на
тях сумата от
втория етаж
![]()
както
и
генерираният
тетраден
пренос pi
трябва да
съответстват
по стойност
на
десетичните. Синтезираните
правила са
разделени на
две групи:
1. Тетрадни
суми без
входящ
пренос от
по-младшия
разряд;
2. Тетрадни
суми с входящ
пренос от
по-младшия
разряд.
Първа
група
правила
Когато
получената
на първия
етаж сума е в
съответствие
с кодовата
таблица 1, тя
не се нуждае
от корекция.
За получаваните
на първия
етаж суми
![]()
на
които не
съответстват
кодови
комбинации,
са
синтезирани
правила за
корекция, сведени
в таблица 3.
Таблица
3.
Корекции на
междинни
суми без
входящ пренос
|
Забранена комбинация |
Корекция
при липса на
пренос от старшия
бит на
тетрадата
|
Корекция
при наличие
на пренос от старшия
бит на
тетрадата
|
|
0
0 1 0 |
+1 |
(-1) или (+1)
ако
|
|
0
1 0 0 |
+1 |
(-1) или (+1)
ако
|
|
0
1 1 0 |
+1 |
(-1) или (+1)
ако
|
|
|
|
|
|
1
0 1 0 |
(+1) или (-1)
ако
|
-1 |
|
1
1 0 0 |
(+1) или (-1)
ако
|
-1 |
|
1
1 1 0 |
(+1) или (-1)
ако
|
-1 |
В
случаите на
корекция на
тетрадната
сума с (-1),
възникналият
на втория
етаж пренос,
не се
разпространява
към
следващата
по-старша
тетрада.
Втора
група
правила
В този
случай към
двете входни
комбинации се
добавя пренос
от по-младшия
разряд
![]()
Правилата
за корекция
за суми,
получени на първия
етаж,
представени
в таблица 3, са
в сила и за
тази група.
В случай, че получената на първия етаж тетрадна сума е в съответствие с кодова таблица 1, тя не се нуждае от корекция. Последното обаче не винаги е вярно, тъй като има случаи, в които сумата е вярна според кодовата таблица, но не е вярна от гледна точка на крайния резултат. Ето защо се налага нова корекция, която да формира крайния резултат в съответствие с десетичния. Тя се извършва в суматора на втория етаж. Според синтезираните за група правила, корекциите в отделните ситуации са две: (+1) или (+2). Конкретните правила са сведени в таблица 4.
Таблица
4.
Корекции на
междинни
суми с входящ
пренос
|
Корекция |
Разпознаващо
правило |
|
+1 |
Когато
получената
тетрадна
сума на
първия етаж
е (0111). Комбинацията
е в
съответствие,
но крайната
сума не е
вярна. |
|
+1 |
Когато
получената
тетрадна
сума на
първия етаж
е (1111), но липсва
тетраден
пренос, т.е.
когато
pi=0. |
|
|
|
|
+2 |
Когато получената тетрадна сума на първия етаж е (0011) и заедно с това старшите битове на двете входни комбинации са еднакви, т.е.
|
|
+2 |
Когато получената тетрадна сума на първия етаж е (0101) и заедно с това старшите битове на двете входни комбинации са еднакви, т.е.
|
|
+2 |
Когато получената тетрадна сума на първия етаж е (1011) или (1101) и заедно с това старшите битове на двете входни комбинации са различни, т.е. когато
|
Във
всички останали
случаи
корекция
няма.
ПРИМЕР 141. Да се съберат числата X=726287 и Y=816769 в код 5211 с кодова таблица 1.
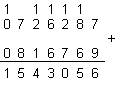
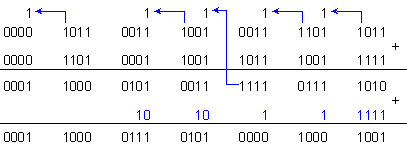
В
горния
пример са
означени
само
тетрадните
преноси.
От
по-горе
изложеното,
аналогично
на вече известните
за други BCD
кодове, така
и тук за код 5211, се
прави извод,
че
логическата
структура на
едноразрядния
суматор в код
5211, ще съдържа два
двоични
4-битови
суматора и
схема за генериране
на
корекциите.
Тази логическа
структура
има вида,
показан на фигура
4.5.2.1.
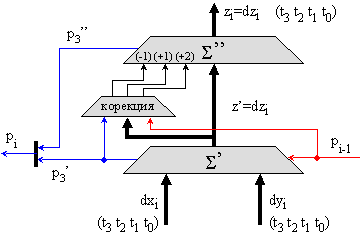
Фиг. 4.5.2.1. Логическа
структура на
едноразряден
BCD суматор в
код 5211 (таблица
2.1)
Схема на
допълнителен
код за кодова
таблица 2.
За
изпълнение
на операция
изваждане е
необходимо
числата със
знак да бъдат
представени
в
допълнителен
код.
Допълнителният
код на
отрицателните
числа може да
се дефинира
чрез
помощния
обратен код,
като сума
![]() .
.
Тъй като
разглеждания
тук тегловен
код не притежава
свойството
допълняемост,
необходимо е да
бъде
синтезирана
специална
схема за неговото
получаване,
която се
основава на определението
за обратен
код
![]()
Определението
(4.5.2.1) се постига
поразрядно
чрез
разликата
![]() )
)
където
с dk е
означена
десетичната
цифра на
числото Х, стояща
в k-ия разряд.
Така в
таблица 5
по-долу, са
изразени
допълненията
на
десетичните
цифри до 9, в
съответствие
с тяхната
кодова таблица
1.
Таблица
5.
Дефиниране
на обратен
код
|
Цифра
|
Допълнение До 9 |
Код
на цифрата
|
Инверсия на
кода |
Корекция |
Код
на допълнението |
|
0 |
9 |
0000 |
1111 |
няма |
1111 |
|
1 |
8 |
0001 |
1110 |
-1 |
1101 |
|
2 |
7 |
0011 |
1100 |
-1 |
1011 |
|
3 |
6 |
0101 |
1010 |
-1 |
1001 |
|
4 |
5 |
0111 |
1000 |
няма |
1000 |
|
5 |
4 |
1000 |
0111 |
няма |
0111 |
|
6 |
3 |
1001 |
0110 |
-1 |
0101 |
|
7 |
2 |
1011 |
0100 |
-1 |
0011 |
|
8 |
1 |
1101 |
0010 |
-1 |
0001 |
|
9 |
0 |
1111 |
0000 |
няма |
0000 |
Както
се вижда
кодът на
допълнението,
т.е. разликата
(4.5.2.3), може да се
получи след
побитова
инверсия на
кодовата
комбинация
на съответната
десетична
цифра и корекция
(-1), ако е
необходимо.
Тъй като
корекцията
трябва да се
постига
автоматично,
за целта
трябва да се
синтезира
логическа
функция за
корекция.
Таблица 5 се
разглежда
като таблица
на истинност,
от която следва
представената
карта на
Карно (фигура
4.5.2.2) и
логическото
уравнение за
функцията на корекция
с (-1).
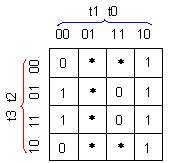
Фиг. 4.5.2.2. Карта
на Карно за
функцията на
корекция с (-1)
![]()
където
с Кт1 е
означена
функцията за
корекция при
кодова
таблица 1.
ПРИМЕР 142. Да се
представи в
допълнителен
код числото Х
= -574906
[X]ПК
= 1
1000 1011 0111
1111 0000 1001
Обратният
код на това
число се
получава от правия
след
побитова
инверсия и
корекция в
съответните
тетради с (-1).

Допълнителният
код се
получава
след прибавяне
на единица
към обратния
код.

ПРИМЕР 143. Да се изпълни операция събиране Z=X+Y, където Х = -574906, Y = 297318. Резултатът трябва да бъде Z = -277588, получен в допълнителен код.
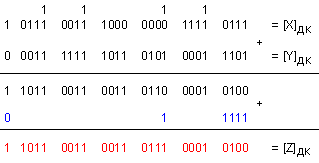
Проверка:

Z = -277588 .
Апаратната реализация на схемата за преобразуване на числа със знак от прав код в допълнителен може лесно да бъде синтезирана въз основа на демонстрираните по-горе правила. На фигура 4.5.2.3 е представена логическа структура на устройство за събиране и изваждане в допълнителен код на BCD-числа, цифрите на които са кодирани в код 5211 в съответствие с кодова таблица 1.
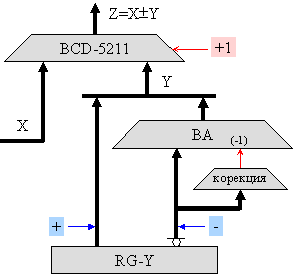
Фиг.
4.5.2.3. Логическа
структура на
многоразряден
2/10-чен
суматор
за
допълнителен
код в BCD код 5211
(таблица 1)
Както
може да се
види,
инверсните
стойности на
битовете на
всяка от
тетрадите на
едно многоразрядно
BCD-число Y, се
вземат от
инверсните изходи
на тригерите
в регистъра. За събиране
с
необходимите
поразрядни
корекции (-1) е
включен
двоичен
суматор ВА (Binary
adder). В
този суматор
липсват
вериги за разпространение
на тетрадни
преноси,
което се
налага от
използвания
допълнителен
код за представяне
на
корекцията (-1).
Практически
той е съставен
от толкова
4-битови
двоични
суматори,
колкото е
дължината на
десетичната
разрядна
мрежа.
За формиране на тетрадните корекции (-1) са включени дешифратори, реализиращи логическа функция (4.5.2.4), синтезирана в съответствие с таблица 5. Добавянето на единица за окончателно формиране на допълнителния код в съответствие с (1), е постигнато по линия на преноса в младшия разряд на BCD-суматора.
Правила
за 2/10-чно
събиране в
код 5211 (кодова
таблица 2)
И тук за
операция
събиране се
налага
синтез на суматор
с двуетажна
логическа
структура. Двоичната
сумата от
първия етаж
![]()
не
винаги е
вярна (в
смисъла на
кодовата таблица).
Във всички
случаи,
когато тя не
е вярна, се
налага
корекция,
стойността
на която се
определя по
силата на представени
по-долу
правила. В
резултат на
тях сумата от
втория етаж
![]()
както
и
генерираният
тетраден
пренос
pi трябва
да
съответстват
по стойност
на десетичните.
И тук
синтезираните
правила са
разделени на
две групи:
1. Тетрадни
суми без
входящ
пренос от
по-младшия
разряд;
2. Тетрадни
суми с входящ
пренос от
по-младшия
разряд.
Първа
група
правила
В случай,
че
получената
на първия
етаж тетрадна
сума е в
съответствие
с кодовата
таблица 2, тя
не се нуждае
от корекция,
с две
изключения.
Изключенията
са вписани в
таблица 6. За
получаваните
на първия
етаж суми
![]()
на които не съответстват кодови комбинации, са синтезирани правила за корекция, сведени също в таблица 6. Вписаните в последните два реда комбинации не са забранени, но не съответстват на правилната сума. В случаи на корекция на тетрадната сума с (-1), възникналият на втория етаж пренос, не се разпространява към следващата по-старша тетрада.
Втора
група
правила
В този
случай към
двете входни
комбинации
се добавя пренос
от по-младшия
разряд
![]()
Таблица
6.
Корекции на
суми без
входящ
пренос
![]()
|
Забранена комбинация |
Корекция
при липса на
пренос от старшия
бит на
тетрадата
|
Корекция
при наличие
на пренос от старшия
бит на
тетрадата
|
|
0
0 1 0 |
+1 |
-1 |
|
0
1 0 0 |
+1 |
-1 |
|
0
1 1 0 |
+1 |
-1 |
|
1
0 0 1 |
+1 |
-1 |
|
1
0 1 1 |
+1 |
-1 |
|
1
1 1 0 |
-1 |
|
|
|
|
|
|
0
0 0 1 |
|
-1 |
|
0
0 1 1 |
|
-2 |
Правилата
за корекция
на суми,
получени на първия
етаж,
представени
в таблица 6, са
в сила и за
тази група.
В случай,
че
получената
на първия
етаж тетрадна
сума е в
съответствие
с кодова
таблица 2, тя
не се нуждае
от корекция.
Последното обаче
не винаги е
вярно, тъй
като има
случаи, в
които сумата е
вярна според
кодовата
таблица, но
не е вярна от
гледна точка
на крайния
резултат. Ето
защо се
налага нова
корекция,
която да формира
крайния
резултат в
съответствие
с десетичния.
Тя се
извършва в
суматора на
втория етаж.
Корекциите в
отделните
ситуации са
три: (+1), (-1) или (+2).
Тези
конкретни
ситуации
правилата са
сведени в
таблица 7.
Таблица
7.
Корекции на
суми с входящ
пренос
![]()
|
Корекция |
Разпознаващо
правило |
|
+1 |
Когато
получената
тетрадна
сума на
първия етаж
е (0110), (0111),
(1011), (1100), (1110)
или (1111). |
|
+1 |
Когато получената тетрадна сума на първия етаж е (0010) или (1001) и липсва тетраден пренос
|
|
|
|
|
-1 |
Когато
получената
тетрадна
сума на
първия етаж
е (0100) |
|
-1 |
Когато получената тетрадна сума на първия етаж е (0010) или (1001) и има тетраден пренос
|
|
|
|
|
+2 |
Когато получената тетрадна сума на първия етаж е (0011) или (0101) и липсва тетраден пренос
|
|
+2 |
Когато
получената
тетрадна
сума на
първия етаж
е (1010) и заедно с
това
|
|
+2 |
Когато
получената
тетрадна
сума на
първия етаж
е (0101) и заедно с
това
старшите
битове на
двете
входни
комбинации
са еднакви,
т.е.
|
Във
всички
останали
случаи
корекция няма.
ПРИМЕР 144.
Да се
съберат
числата X=726287 и Y=816719
в код 5211 с
кодова
таблица 2.
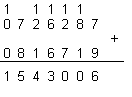
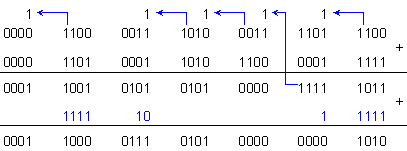
В
горния
пример са
означени
само
тетрадните
преноси.
От
изложеното в
този раздел, аналогично
на случая
според
кодова таблица
1, се прави
извод, че
логическата
структура на
едноразрядния
суматор в код
5211 за кодова
таблица 2, ще
съдържа два
двоични
4-битови суматора
и схема за
генериране
на корекциите.
Тази
логическа
структура
има вида,
показан на
фигура 4.5.2.4.
Логическата
структура на
суматора в
съответствие
с кодова
таблица 2
реализира
една корекция
в повече (-2) в
сравнение с
тази, синтезирана
в
съответствие
с таблица 1.
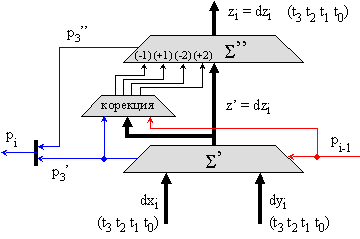
Фиг.
4.5.2.4. Логическа
структура на
едноразряден
BCD суматор в
код 5211 (таблица
2)
Схема
на
допълнителен
код за кодова
таблица 2
Изложеното
в раздела,
който се
отнася за кодова
таблица 1,
относно
изпълнението
на операция
изваждане, е
напълно
аналогично и
в този
случай. В
сила са определения
(4.5.2.1) и (4.5.2.2). В
таблица 8
по-долу са
изразени
допълненията
на
десетичните
цифри до 9, в съответствие
с тяхната
кодова
таблица 2.
Таблица
8.
Дефиниране
на обратен
код
|
Цифра
|
Допълнение до
9 |
Код
на цифрата
|
Инверсия на
кода |
Корекция |
Код
на допълнението |
|
0 |
9 |
0000 |
1111 |
|
1111 |
|
1 |
8 |
0001 |
1110 |
-1 |
1101 |
|
2 |
7 |
0011 |
1100 |
|
1100 |
|
3 |
6 |
0101 |
1010 |
|
1010 |
|
4 |
5 |
0111 |
1000 |
|
1000 |
|
5 |
4 |
1000 |
0111 |
|
0111 |
|
6 |
3 |
1010 |
0101 |
|
0101 |
|
7 |
2 |
1100 |
0011 |
|
0011 |
|
8 |
1 |
1101 |
0010 |
-1 |
0001 |
|
9 |
0 |
1111 |
0000 |
|
0000 |
Както се
вижда, кодът
на
допълнението
може да се
получи след
побитова
инверсия на
кодовата
комбинация
на
съответната
десетична
цифра и
корекция (-1),
ако е
необходимо.
Тъй като
корекцията
трябва да се
постига
автоматично,
за целта се
синтезира
логическа
функция за
корекция. От таблица
8 като
таблица на
истинност
следва представената
карта на
Карно (фигура
4.5.2.5) и логическото
уравнение за
функцията на
корекция с (-1).
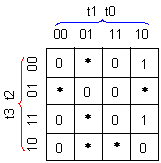
Фиг. 4.5.2.5. Карта
на Карно за
функцията на
корекция с (-1)
![]()
където
с Кт2 е
означена
функцията за
корекция при
кодова
таблица 2.
ПРИМЕР
145. Да се
представи в
допълнителен
код числото Х =
-514816 .
[X]ПК = 1 1000
0001 0111 1101
0001 1010
Обратният
код на това
число се
получава от правия
след
побитова
инверсия и
корекция в
съответните
тетради с (-1).
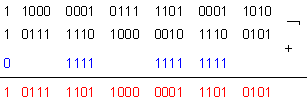
Допълнителният
код се
получава
след прибавяне
на единица
към обратния
код.

ПРИМЕР
146. Да се
изпълни
операция
събиране Z=X+Y,
където Х = -514816, Y =
287318.
Резултатът
трябва да
бъде Z =
-227498,
получен в
допълнителен
код.
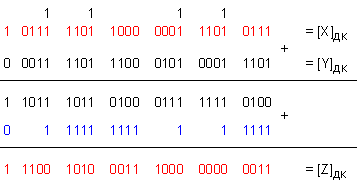
Проверка:

Z = -227498
.
Схемата
за преобразуване
на числа със
знак от прав
код в допълнителен,
както и
използването
й за изпълнение
на операция
изваждане, е
аналогична
на
логическата
структура,
представена на
фигура 4.5.2.3.
Разликата в
нея е в това,
че дешифраторите,
които
формират
тетрадните
корекции,
реализират
логическа
функция (4.5.2.5),
синтезирана
в
съответствие
с таблица 8.
Заключение
Изложеното
проучване
показва, че
двоичната
аритметика
отстъпва все
повече място
на
десетичната.
Това се дължи
от една
страна на
възможностите
на технологиите
за
реализация, а
от друга
страна на реалната
необходимост.
Десетичен
хардуер вече
се реализира
както в
традиционни
микропроцесорни
системи, така
и в схеми с
програмируема
логика.
Самата кухня
е разнообразна,
което
означава, че
в изминалите
няколко години
все още не е
постигнато
единодушие и
в научно
направление
изследванията
продължават.
Броят
на 4-битовите
тегловно
значими
двоично-десетични
кодове е
значителен
29059430400, което означава,
че
търсенията
на учените
вероятно все
още
продължават.
В
първи раздел
беше
отбелязано,
че кодът 5211 има
своите
достойнства,
за да бъде
избран. Но и
самият той
предлага
достатъчно
разнообразие,
за да не се
счита това
изследване
за окончателно.
От
възможните 64
кодови
таблици за код
5211, тук са
представени
техническите
решения само
за две.
Резултатите
са достатъчни
за да се
направи
избор в полза
на решението,
съответстващо
на кодова
таблица 1. Краткото
изложение е
показателно
за обема на
усилията,
които ще
следва да се
положат, ако
читателят
реши да
изследва
пълното множество
от възможни
кодови
таблици.
Следващият
раздел е:
4.6
Умножение
на двоично
десетични числа