IV.8 Преобразуване на числа от една бройна система в друга
Алгоритмите,
които ще
бъдат
демонстрирани
тук, са
съобразени с
тяхната
машинна реализация.
IV.8.1
Преобразуване
от десетична
в двоична бройна
система
А)
ПРЕОБРАЗУВАНЕ
НА ЧИСЛА С
ДЯСНО ФИКСИРАНА
ЗАПЕТАЯ
ПРИМЕР
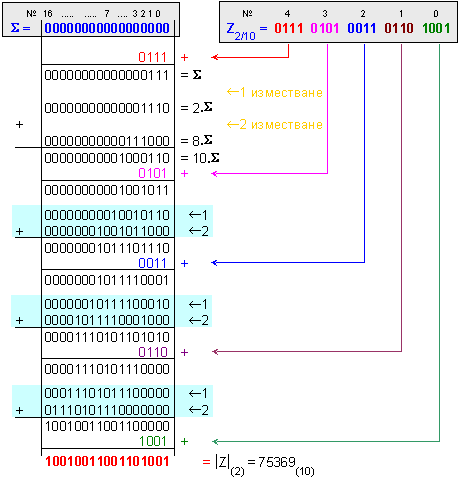
150.
Да се намери
двоичният
еквивалент на
цялото
число Z=75369, .
Прилагайки
съответната
формула за
определяне
дължината на
двоичното
поле (вижте
в книга [1]),
което следва
да побере
двоичния
еквивалент,
получаваме:
n ³ 5
[разряда] * 3,3222591 =
16,6112955 [b]
Получената
стойност
означава, че
двоичното
поле, което
може да
побере
даденото
5-разрядно
десетично
число, трябва
да бъде не по-късо
от 17[b].
Б)
ПРЕОБРАЗУВАНЕ
НА ЧИСЛА С
ЛЯВО ФИКСИРАНА
ЗАПЕТАЯ
ПРИМЕР 151.
Да се намери
двоичният
еквивалент на
числото с
ЛФЗ Z=0,789 .
Прилагайки
същата
формула за
определяне дължината
на двоичното
поле,
получаваме:
n ³ 3
[разряда] * 3,3222591 =
9,9667773 [b]
Получената
стойност
означава, че
двоичното
поле, което
може да
побере
даденото
3-разрядно
десетично
число, трябва
да бъде не по-късо
от 10[b].
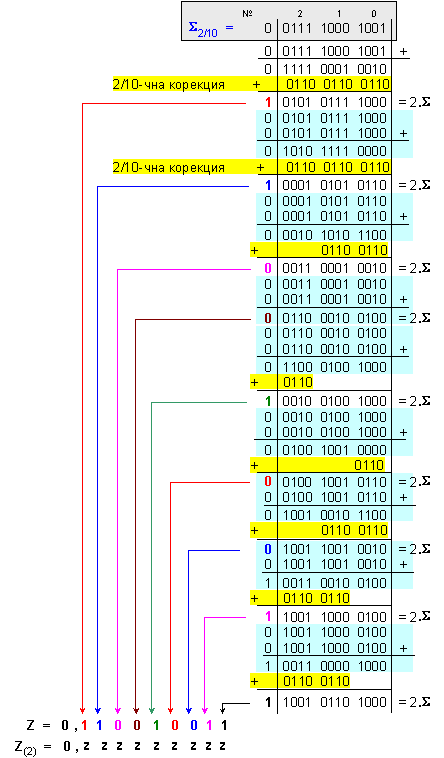
Този
резултат:
![]()
е по-малък (с
недостиг) от
изходното
число. Това
се дължи от
една страна
на
недостатъчната
дължина на
двоичното
поле, а от
друга страна
на това, че преобразованието
не винаги е
точно.
Следващият
раздел е:
4.8.2
Преобразуване
от двоична в
десетична
бройна
система