Последната редакция на тази книга е от 2021 година.

V. ЧИСЛА С ПЛАВАЩА ЗАПЕТАЯ

Примерите представени в този раздел илюстрират операции върху числа представени във форма с плаваща запетая в стандарта с изместен порядък, както без, така и с техниката на скрития бит. Това означава, че като нормализирана мантиса М тук ще се приема всяко число, намиращо се в интервала:

0,1 £ |М| < 1,0

или

1,0 £ |М| < 2,0

когато се използва техниката на скрития бит.

V.1 Операции събиране и изваждане на числа с плаваща запетая

Трябва да предупредим читателя, че към представените числени примери в този и в следващите раздели следва да подхожда след добра подготовка и детайлно запознаване с теоретичните постановки и със свързаните с тях алгоритми, които са изложени подробно в книга [1].

ПРИМЕР 154. Да се определят параметрите на разрядната мрежа, представяща числа във форма с плаваща запетая при следната организация: обща дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Разрядната мрежа, определена в задачата, има следната структура:

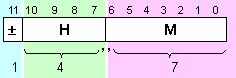
Всяко число X, което се представя в нея има следния вид:

Мантисата е нормализирано число с ляво фиксирана запетая, представено в прав код, предхождано от знака на числото. Характеристиката е цяло число без знак, а порядъкът е разликата между характеристиката и отместването D. Отместването е равно на теглото на най-старшия разряд в полето на характеристиката. За нашия пример, при k=4[b], се получава

Така диапазонът на възможните характеристики е [0¸15], което съответствува на интервала [-8¸7] на възможните за това поле порядъци. Диапазонът на представимите в разрядната мрежа числа

се определя от числата:

Най-близките до нулата числа са:

Относителната погрешност на така определената разрядна мрежа се изчислява по формулата:

където q е основата на бройната система. В условията на нашия пример относителната погрешност е

Числата, които се представят в разрядната мрежа без загуба, т.е. точно, имат относителна погрешност d=0.

Всяко число, имащо порядък по-голям от +7, е непредставимо в дадената разрядна мрежа и получаването му води до генериране на признак “препълване при плаваща запетая”.

Всяко число, имащо порядък по-малък от –8, е непредставимо в дадената разрядна мрежа и получаването му води до генериране на признак “антипрепълване”, като за окончателен резултат се приема числото “машинна нула”, която е числото

ПРИМЕР 155. Да се изпълни операция събиране Z=X+Y на числата X=-71 и Y=49, които са представени в разрядна мрежа с дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

При тази дължина на полето за характеристиката (4 [b]), отместването е D=2³=8. Във форма с плаваща запетая числото X има вида:

Този вид на числото се характеризира с нормализираната мантиса. За да се попълни разрядната мрежа е необходимо да се получи характеристиката на числото, т.е. H=p+D=+7+8=15.

Второто число:

се представя по същия начин. Неговата характеристика се определя така: H = p+D = 6+8 = 14.

Така представените числа встъпват в операция събиране. Тъй като числото Y има по-малка характеристика

за характеристика на резултата се приема тази на числото X, a в етапа “изравняване на порядъците”, мантисата на Y се измества надясно на 1 разряд и приема вида:

0,0110001

след което се извършва събирането:

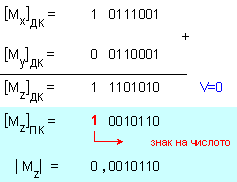
Както се вижда, събирането е извършено в допълнителен код. Това е така, защото знаците на числата се “носят” от мантисите. Втората част на примера представя превръщането на получената сума в прав код, който съдържа модула на числото. Получената сума не е нормализирано число ето защо чрез две измествания наляво тя се нормализира, т.е.

При това от характеристиката се изваждат последователно две единици и тя получава стойността H=15-2=13, 13=1101₍₂₎. Така окончателно от знак, характеристика и мантиса се сглобява съдържанието на разрядната мрежа, представящо получената сума:

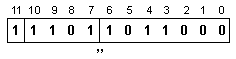
Според формата за представяне, това съдържание съответствува на следното число:

ПРИМЕР 156. Да се изпълни операция събиране Z=X+Y на числата X=10,5 и Y=99,625 , които са представени в разрядна мрежа с дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Резултатът от събиране на двете числа е: Z = X+Y = 10,5+99,625 = 110,125. Във форма с плаваща запетая числата се представят както следва:

.

Характеристиката на това число е H=4+8=12. Съдържанието на разрядната мрежа ще бъде следното:

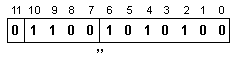
Характеристиката на това число е H=7+8=15. За съжаление значещата част на това число е по-дълга от възможностите на разрядната мрежа, която има дължина от 7 бита, в резултат на което 3 младши бита няма да бъдат представени, както илюстрира следващата рисунка:

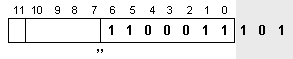
Така числото Y ще бъде представено неточно. Допуснатата грешка е принципна и не може да бъде отстранена. Съдържанието на разрядната мрежа ще бъде следното:

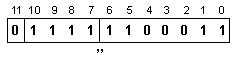
Така представените числа встъпват в операция събиране. Тъй като числото X има по-малка характеристика

за характеристика на резултата се приема тази на числото Y, a в етапа “изравняване на порядъците”, мантисата на X се измества надясно спрямо запетаята на 3 разряда и приема вида:

0,0001010

след което се извършва събирането:

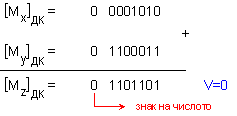
Вижда се, че получената сума е нормализирано число. Така окончателно от знак, характеристика и мантиса се сглобява съдържанието на разрядната мрежа, представящо получената сума:

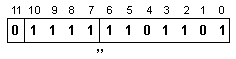
Според формата за представяне, това съдържание съответствува на следното число

ПРИМЕР 157. Да се изпълни операция събиране Z=X+Y на числата X=0,11001.2⁺⁷ и Y=0,11101.2⁺⁵ , които са представени в разрядна мрежа с дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Числата имат следното изображение в разрядната мрежа:

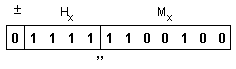
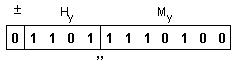
Тъй като характеристиката на второто число е по-малка от тази на първото число (15>13), то за изравняване на порядъците, мантисата M_y ще се измести на 2 разряда надясно, при което ще загуби 2 младши бита и ще добие вида:

0,0011101 00

След това се извършва събирането:

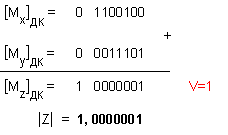
Вижда се, че при събиране на двете положителни числа, е настъпило положително препълване. По същество получената сума е число по-голямо от единица, т.е. ненормализирано число. За да бъде нормализирано следва да се измести на един бит надясно, при което приема вида:

0,1000000 1

При това тя губи един бит от десния си край, което е принципна грешка, т.е. неизбежна. За запазване на същото количество към характеристиката се прибавя една единица и тя получава стойността H=15+1=16=10000. Тази сума обаче е число, което е непредставимо в четирибитовото поле на характеристиката, ето защо в този случай се генерира окончателно признак за препълване при плаваща запетая.

ПРИМЕР 158. Да се изпълни събиране Z=X+Y на числата X=0,11001.2^-4 и Y=-0,1100111.2^-4 , които са представени в разрядна мрежа с дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Числата имат следното изображение в разрядната мрежа:

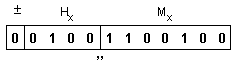
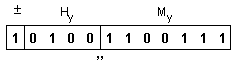
Тъй като характеристиката на първото число е равна на характеристиката на второто число, то етапа “изравняване на порядъците” в алгоритъма на операция събиране за този пример се прескача и следва събирането на мантисите в допълнителен код:

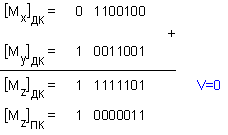
Получената сума е отрицателно число без препълване, което е ненормализирано. За да стане нормализирано трябва да се измести на 5 бита наляво, при което се получава следната мантиса:

В процеса на нормализиране на мантисата, след всяко нейно изместване наляво на един бит, от характеристиката се изважда единица, т.е.

Така на петото изместване ще се получи отрицателно препълване и стойност за характеристиката

която не може да се представи. Като цяло полученото с плаваща запетая число е непредставимо, но тъй като е много близко до числото нула, за окончателен резултат се приема числото “машинна нула”, което се представя по следния начин:

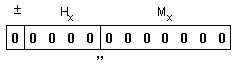
който съответства на стойността:

ПРИМЕР 159. Да се изпълни операция изваждане Z=X-Y на числата X=0,1100101.2^-2 и Y=0,1110111.2⁺³ , които са представени в разрядна мрежа с дължина n=16[b]=m+k, където k=5[b] е дължината на полето за представяне на характеристиката, а m=11[b] е дължината на полето за представяне на мантисата.

Определената в примера разрядна мрежа може да представя характеристики в диапазона [00000¸11111], което съответствува на [0¸31] или още на порядъците в диапазона [-16¸+15]. Следователно отместването D на порядъка в тази разрядна мрежа ще бъде равно на 16=2^(k-1)=2⁴.

Характеристиката на първото число ще бъде следната: H_x=-2+16=14, a на второто число ще бъде: H_y=3+16=19. При тези стойности числата ще бъдат представени в разрядната мрежа по следния начин:

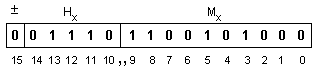
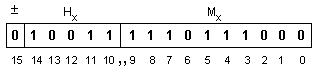
Операция изваждане започва със сравнение на характеристиките. В случая характеристиката на първото число е по-малка от тази на второто число, ето защо мантисата M_x ще се измести надясно на 5 бита и ще приеме вида:

0,0000011001 01000

при което ще изгуби младшата си част, която в случая е значеща. Това означава, че не може да се очаква точен резултат. Грешката е неизбежна, т.е. принципна. Ако в даден случай разликата между характеристиките е по-голяма от числото (m-1), изместването надясно на съответната мантиса може да доведе до нейната загуба. В книга [1] беше пояснено, че в този случай съответното число губи своето значение, т.е. приема се за нула, което се отбелязва с вдигане на флаг в АЛУ.

Операция изваждане на двете мантиси се изпълнява в допълнителен код:

Мантисата на получената сума е нормализирана, ето защо операцията завършва със сглобяване на съдържанието на разрядната мрежа:

Резултатът е числото

Z = -0,1110011111.2⁺³ = -111,0011111.

Следващият раздел е:

5.2 Операция умножение на числа с плаваща запетая