Последната редакция на тази книга е от 2021 година.

V.2 Операция умножение на числа с плаваща запетая

ПРИМЕР 160. Да се изпълни операция умножение Z=X.Y на числата X=0,1001.2⁺² и Y=0,1001.2⁺³ , които са представени в разрядна мрежа с обща дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 0 1010 1001000 ; Y Þ 0 1011 1001000 .

Характеристиките на числата се събират по следния начин:

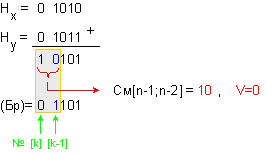
При това събиране няма препълване и тригерът на препълването остава в състояние нула (ТП=0). Така получената на изхода на суматора сума се коригира автоматично при записването си в брояча на характеристиките БрН (вижте книга [1]). Броячът приема стойността (Бр)=0 1101, където в неговия най-старши k-ти разряд се записва нула, а в (k-1)-я разряд отрицанието:

След първоначалното събиране и коригиране на характеристиките следва умножението на двете положителни мантиси, които са числа с ляво фиксирана запетая. По-долу то е извършено по метода с младшите разряди напред, по схемата с неподвижно множимо, по модул:

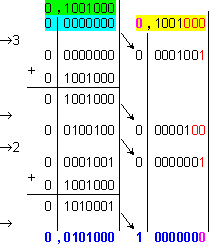
Получената мантиса

е число с двойна дължина (16 бита). Освен това то е ненормализирано, което налага неговото изместване наляво на един бит наляво. Така мантисата

става нормализирана и след отрязване на младшите й цифри тя може да се запише с единична дължина в разрядната мрежа, т.е.

Следва да се разбира, че ако в отхвърлената младша част има значещи цифри, това води до съответната грешка. Тя е неизбежна и може да се намали само след закръгляне.

Нормализацията на произведението изисква изваждане на една единица от характеристиката на резултата, което се извършва в брояча на характеристиките и тя става

Така всички елементи на структурата на разрядната мрежа са получени и произведението може да бъде сглобено окончателно:

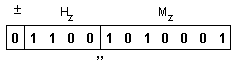
Изобразеното съдържание представлява числото:

ПРИМЕР 161. Да се изпълни операция умножение Z=X.Y на числата X=0,1001.2⁺² и Y=-0,1001.2^-4, които са представени в разрядна мрежа с обща дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 0 1010 1001000 ; Y Þ 1 0100 1001000 .

Характеристиките на числата се събират по следния начин:

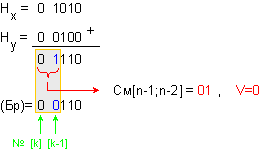
При това събиране няма препълване и тригерът на препълването остава в състояние нула (ТП=0). Така получената на изхода на суматора сума се коригира автоматично при записването си в брояча на характеристиките (виж фигура 3.28 на книга [1]). Броячът приема стойността (Бр)=0 0110, където в неговия най-старши разряд се записва нула, а в по-младшия:

След първоначалното събиране и коригиране на характеристиките следва умножението на двете мантиси. То е извършено по модул.

Получената мантиса

е число с двойна дължина (16 бита). Освен това то е ненормализирано, което налага неговото изместване наляво на един бит. Така мантисата става нормализирана

и след отрязване на младшите й цифри тя може да се запише с единична дължина в разрядната мрежа, т.е.

Нормализацията на произведението изисква изваждане на една единица от характеристиката на резултата, което се извършва в брояча на характеристиките БрН и тя става

Така всички елементи на структурата на разрядната мрежа са получени и произведението може да бъде сглобено окончателно:

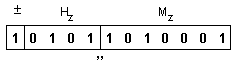
Изобразеното съдържание представлява числото:

ПРИМЕР 162. Да се изпълни операция умножение Z=X.Y на числата X=0,1100101.2⁺⁹ и Y=0,1110111.2⁺⁸, които са представени в разрядна мрежа с дължина n=16[b]=m+k, където k=5[b] е дължината на полето за представяне на характеристиката, а m=11[b] е дължината на полето за представяне на мантисата.

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 0 11001 1100101000 ; Y Þ 0 11000 1110111000 .

Характеристиките на числата се събират по следния начин:

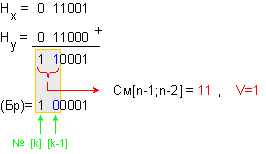
При това събиране настъпва положително препълване в полето на характеристиките, което тригерът на препълването регистрира (ТП=1). Така получената на изхода на суматора сума се коригира автоматично при записването си в брояча на характеристиките. Броячът приема стойността (Бр)=1 00001, където

След първоначалното събиране и коригиране на характеристиките следва умножението на двете мантиси. В този пример то е извършено по алгоритъма на Бут.

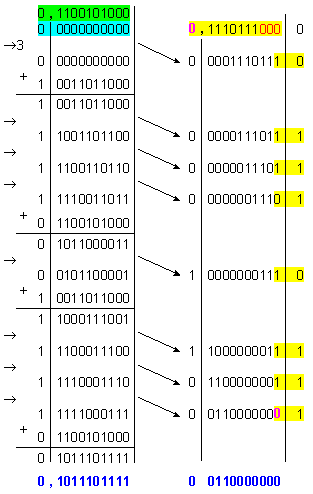
Получената мантиса

е число с двойна дължина (22 бита). Тъй като числото се получава като нормализирано, това не налага неговото изместване. След отрязване на младшите цифри, мантисата може да се запише с единична дължина в разрядната мрежа, т.е.

Така съдържанието на брояча на характеристиките остава непроменено, т.е. (Бр) = 1 00001.

Това съдържание обаче е по-голямо от възможната максимална стойност в полето на характеристиката. Препълването на това поле се сигнализира от единицата, стояща все още в най-старшия разряд на брояча. В резултат на това числото с плаваща запетая е непредставимо и се генерира признак за препълване при плаваща запетая. Полученото следва да се разбира като положителна безкрайност .

ПРИМЕР 163. Да се изпълни операция умножение Z=X.Y на числата X=0,101.2⁺⁸ и Y=0,11.2⁺⁸, които са представени в разрядна мрежа с дължина n=16[b]=m+k, където k=5[b] е дължината на полето за представяне на характеристиката, а m=11[b] е дължината на полето за представяне на мантисата.

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 0 11000 1010000000 ; Y Þ 0 11000 1100000000 .

Характеристиките на числата се събират по следния начин:

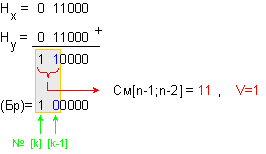
При това събиране настъпва положително препълване в полето на характеристиките, което тригерът на препълването регистрира (ТП=1). Така получената на изхода на суматора сума се коригира автоматично при записването си в брояча на характеристиките. Броячът приема стойността (Бр)=1 00000, където

След първоначалното събиране и коригиране на характеристиките следва умножението на двете мантиси. Произведението е получено по алгоритъма на Бут:

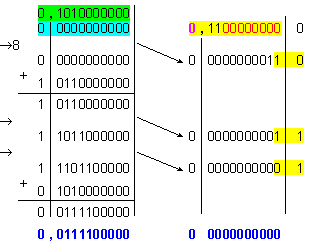
Получената мантиса

е число с двойна дължина (22 бита). Освен това то е ненормализирано, което налага неговото изместване наляво на един бит. Така мантисата става нормализирана и след отрязване на младшите й цифри тя може да се запише с единична дължина в разрядната мрежа, т.е.

Нормализацията на произведението изисква изваждане на една единица от характеристиката на резултата, което се извършва в брояча на характеристиките и тя става

Така след нормализацията на мантисата на произведението препълването в полето на характеристиката се отнема, което се разпознава по това, че k-тият разряд на брояча се нулира, т.е. положителното препълване в този пример е било само на един порядък.

Така всички елементи на структурата на разрядната мрежа са получени и произведението може да бъде сглобено окончателно:

Изобразеното съдържание представлява числото:

ПРИМЕР 164. Да се изпълни операция умножение Z=X.Y на числата X=0,101.2^-9 и Y=0,11.2^-10, които са представени в разрядна мрежа с дължина n=16[b]=m+k, където k=5[b] е дължината на полето за представяне на характеристиката, а m=11[b] е дължината на полето за представяне на мантисата.

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 0 00111 1010000000 ; Y Þ 0 00110 1100000000 .

Характеристиките на числата се събират по следния начин:

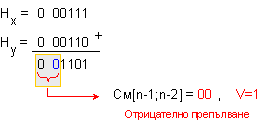
При настъпване на отрицателно препълване в полето на характеристиката, умножението на мантисите може да се прескочи, тъй като това препълване не може да се отстрани със следващата евентуална нормализация на мантисата, напротив чрез нея то ще се засили. В този случай за резултат се приема машинната нула и се генерира признак “антипрепълване”, т.е. съдържанието на разрядната мрежа е следното:

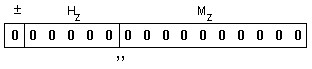
Следващият раздел е:

5.3 Операция деление на числа с плаваща запетая