Последната редакция на тази книга е от 2021 година.

V.3 Операция деление на числа с плаваща запетая

Отново ще предупредим читателя, че към представените числени примери в този, така и във всички следващите раздели следва да подхожда след добра подготовка и детайлно запознаване с теоретичните постановки и свързаните с това алгоритми, които са изложени подробно в книга [1].

ПРИМЕР 165. Да се изпълни операция деление Z=X/Y на числата X=0,1101.2⁺⁴ и Y=-0,1011.2⁺², които са представени в разрядна мрежа с обща дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 0 1100 1101000 ; Y Þ 1 1010 1011000 .

Характеристиките на числата се изваждат по следния начин:

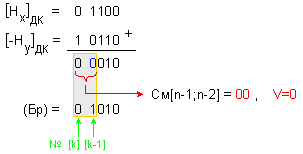
При това изваждане няма препълване и тригерът на препълването остава в състояние нула (ТП=0). Така получената на изхода на суматора сума се коригира автоматично при записването си в брояча на характеристиките (виж фигура 3.28 на [1]). Броячът приема стойността (Бр)=01010, където в неговия най-старши разряд се записва нула, а в по-младшия стойността:

След първоначалното събиране и коригиране на характеристиките следва делението на двете мантиси, които припомняме, са числа с ляво фиксирана запетая. То е извършено по метода без възстановяване на остатъците, по схемата с неподвижен делител по модул:

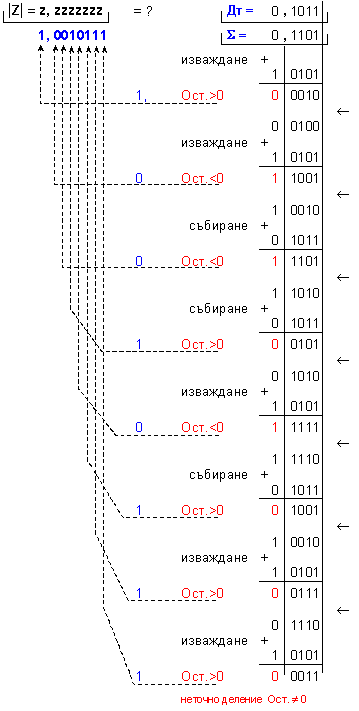
Полученото частно

е число по-голямо от единица. Това число следва да се нормализира като се измести на един разряд надясно. Отново обръщаме внимание на загубата на младша значеща цифра, което е неизбежно и представлява принципна грешка. За стойността на мантисата остава числото

Извършената нормализация на мантисата на частното чрез изместване надясно води до корекция на характеристиката, която се увеличава с единица. Корекцията се извършва в брояча на характеристиката, като съдържанието му приема стойността

(Бр) = 01010+1 = 01011 .

Така окончателно от знак, характеристика и мантиса в разрядната мрежа се сглобява резултатът:

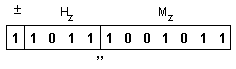
Това съдържание представя числото:

Z = -0,1001011.2^(11-8) = -100,1011 = -4,6875 .

Този резултат се различава от по-точния, който е -4,72(72)…. Това се дължи на неточното деление и на загубата на значеща цифра при нормализацията на мантисата на частното. Заедно с тази цифра частното би било числото 100,10111 = -4,71875 , което, както се вижда, е по-близо да истината.

ПРИМЕР 166. Да се изпълни операция деление Z=X/Y на числата X=0,1101.2^-4 и Y=-0,1011.2⁺⁵, които са представени в разрядна мрежа с обща дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 0 0100 1101000 ; Y Þ 1 1101 1011000

Характеристиките на числата се изваждат по следния начин:

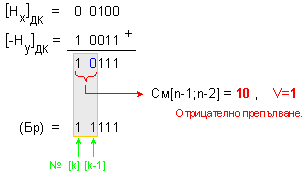
В случай като този, когато при изваждане на характеристиката на делителя от тази на делимото настъпи отрицателно препълване, същото следва да се регистрира в тригера на препълването (ТП:=1). Тогава броячът на характеристиката приема и цифрата в k-тия разряд. Чрез тази цифра ще се установи дали това препълване е премахнато след нормализацията на мантисата на частното. Ако този бит не промени стойността си и остане в единица, това означава, че е настъпило “антипрепълване” и за резултат ще трябва да се приеме числото “машинна нула”.

След разделяне на мантисите, както е показано в преидущия пример, се вижда, че полученото частно

е число по-голямо от единица. Това число следва да се нормализира като се измести на един разряд надясно. При това то губи младшия си бит и приема стойността

Извършената нормализация на мантисата на частното води до корекция на характеристиката, която се увеличава с единица, като съдържанието на брояча приема стойността

(Бр) = 11111+1 = 00000 .

При това тук в този пример, k-тият разряд на брояча се нулира ((Бр.[k])=0), от което се разбира, че отрицателното препълване в полето на характеристиката е компенсирано (отнето).

Така окончателно от знак, характеристика и мантиса в разрядната мрежа се сглобява резултатът:

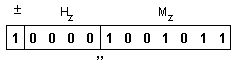
Това съдържание представя числото:

ПРИМЕР 167. Да се изпълни операция деление Z=X/Y на числата X=-0,11011.2⁺⁵ и Y=-0,10011.2^-2, които са представени в разрядна мрежа с обща дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 1 1101 1101100 ; Y Þ 1 0110 1001100

Характеристиките на числата се изваждат по следния начин:

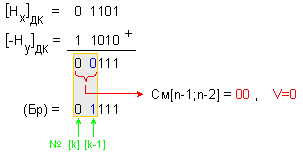
При това изваждане няма препълване и тригерът на препълването остава в състояние нула (ТП=0). Така получената на изхода на суматора сума се коригира автоматично при записването си в брояча на характеристиките. Броячът приема стойността (Бр)=01111, където в неговия най-старши разряд се записва нула, а в по-младшия – стойността:

След първоначалното събиране и коригиране на характеристиките следва делението на двете мантиси. То е извършено по метода без възстановяване на остатъците по схемата с неподвижен делител по модул чрез алгоритъма на малките остатъци. Знаците на операндите са формирали знака на частното предварително.

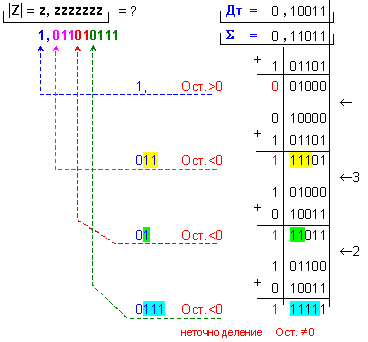
При разделяне на мантисите полученото число

е по-голямо от единица. Освен това е получено с два допълнителни разряда. Това число следва да се нормализира като се измести на един разряд надясно. За да не загуби от точността си, т.е. младшите три бита, ще извършим закръгление и мантисата ще приеме стойността

Извършената нормализация на мантисата на частното води до корекция на характеристиката, която се увеличава с единица, като съдържанието на брояча приема стойността

(Бр) = 01111+1 = 10000 .

При това тук, в този пример, k-тият разряд на брояча приема единица, от което се разбира, че той се препълва.

Окончателно става ясно, че полученото частно е прекалено голямо число и не може да се представи в така дадената разрядна мрежа. В резултат на това се генерира признак за “препълване при плаваща запетая”.

ПРИМЕР 168. Да се изпълни операция деление Z=X/Y на числата X=-0,11011.2⁺⁵ и Y=-0,10011.2^-5, които са представени в разрядна мрежа с обща дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 1 1101 1101100 ; Y Þ 1 0011 1001100 .

Характеристиките на числата се изваждат по следния начин:

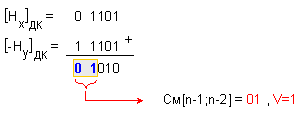
При това изваждане настъпва дълбоко препълване в полето на характеристиката, което тригерът на препълването регистрира (ТП=1). Това препълване не може да бъде отнето, а напротив, в случай на препълване в полето на мантисата, както в предидущия пример, то може да бъде само засилено! Ето защо делението в този случай завършва с генериране на признак “препълване при плаваща запетая”.

ПРИМЕР 169. Да се изпълни операция деление Z=X/Y на числата X=0,11.2^-2 и Y=0,11.2⁺², които са представени в разрядна мрежа с обща дължина n=12[b]=m+k, където k=4[b] е дължината на полето за представяне на характеристиката, а m=8[b] е дължината на полето за представяне на мантисата.

Резултатът от това деление е следният:

Числата са представени в разрядната мрежа от следните комбинации:

X Þ 0 0110 1100000 ; Y Þ 0 1010 1100000 .

Характеристиките на числата се изваждат по следния начин:

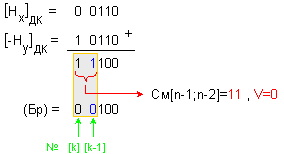
Полученото частно

е число равно на единица. Това число следва да се нормализира като се измести на един разряд надясно като приема стойността

Извършената нормализация на мантисата на частното чрез изместване надясно води до корекция на характеристиката, която се увеличава с единица, като съдържанието на брояча приема стойността

(Бр) = 00100+1 = 00101 .

Така окончателно от знак, характеристика и мантиса в разрядната мрежа се сглобява резултатът:

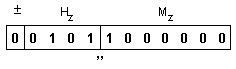
Това съдържание представя числото:

Следващият раздел е:

5.4 Операции върху числа, представени във форма с плаваща запетая чрез техниката на скрития бит