V.4
Операции
върху числа,
представени във
форма с
плаваща
запетая чрез
техниката на
скрития бит
Според
техниката на
скрития бит,
представена
подробно в книга [1], при
представяне
на едно число
във форма с
плаваща
запетая е
необходимо
да се уточни
предварително
неговия
формат в два аспекта:
a Дали
става въпрос
за
представяне
на числото в
паметта,
когато се
използува
така нареченият
“Memory format” (MemF),
или става
въпрос за
представяне
на числото в
АЛУ при
изпълнение
на операция – “Operation format” (OpF);
a Кой от
форматите по
отношение на
точността се
има предвид (Single, Double
или Extended Precision), (SP, DP, EP).
При
съхраняване
на числата в
паметта скритият
бит
присъства
единствено
във формата Extended Precision.
Когато
числата се
извличат от
паметта и се подготвят
за участие в
операция в
АЛУ, те съдържат
скрития бит
представен
явно в състава
на мантисата
на числото.
Възстановената
в явен вид
старша
единица на
мантисата се
появява отляво
на запетаята,
ето защо
нормализираната
мантиса на
подготвеното
за операция
число има
вида:
![]()
Така
възможните
гранични
стойности на
двоичната
мантиса са:
![]()
В
резултат на
това
положение на
запетаята на
мантисата, в
чиято цяла
част винаги
има една
цифра, отместването
на порядъка е
с една
единица
по-малко.
Тогава
характеристиката
на така
представяните
числа се
получава по
формулата:
H = p+(D-1) = p+(2(k-1)-1) . (98)
Граничните
стойности на
характеристиката:
H=0 и H=max са
резервирани
за изобразяване
на изключителните
ситуации.
Стойността H=0
се използува
за
представяне на
числото “нула”,
а стойността
H=max за
представяне
на абстракциите
“безкрайност”
и “NAN”.
ПРИМЕР 170. Да се
изпълни
операция
събиране Z=X+Y
на
числата X=-71 и
Y=49, които
са
представени
в разрядна
мрежа с обща
дължина n=12[b]=m+k, където k=4[b] е
дължината на
полето за
представяне
на характеристиката,
а m=8[b] е
дължината на
полето за
представяне
на мантисата
(без скрития
бит).
При тази
дължина на
полето за
характеристиката
(4 [b]),
отместването
е
![]()
Във
форма с
плаваща
запетая
числото X има
вида:
![]()
т.е.
![]()
Последният
вид на
числото се
характеризира
с мантиса,
която е
нормализирана
в смисъла на
техниката на
скрития бит.
За да
се попълни
разрядната
мрежа с
изображението
на числото X
е необходимо
да се получи
характеристиката
на числото,
т.е.
![]() .
.
И
така,
подготвеното
за операция число
има вида:
![]()
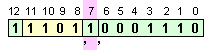
при
който се
вижда явно
изобразената
цифра в
цялата част
на мантисата,
заради която
дължината на
разрядната
мрежа е
увеличена с
единица: n+1=(m+1)+k.
Второто
число
![]()
се
представя по
същия начин.
Характеристиката
му се
определя
така:
![]() .
.
Подготвеното
за операция
число има
вида:
![]()
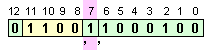
Така
представените
числа
встъпват в
операция
събиране. Тъй
като числото Y
има по-малка
характеристика
![]()
за
характеристика
на резултата
се приема тази
на числото X, a в
етапа “изравняване
на
порядъците”,
мантисата на Y
се измества
надясно на 1
разряд и
приема вида:
+0,1100010 ,
след
което се
извършва
събирането:
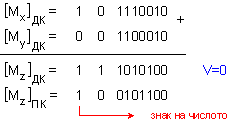
Получената
сума не е
нормализирано
число в
смисъла на
скрития бит,
ето защо чрез
две измествания
наляво тя се
нормализира,
т.е.
![]()
При
това от
характеристиката
се изваждат последователно
две единици и
тя получава
стойността
![]()
Така
окончателно
от знак,
характеристика
и мантиса се
сглобява
съдържанието
на разрядната
мрежа,
представящо
получената
сума:
![]()
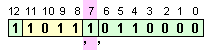
Когато
получената
сума се
записва в
оперативната
памет на
процесора, тя
ще получи
следния вид:
![]()
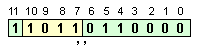
в който
липсва
старшата
единица
(цялата част
на
мантисата).
Според
формата за
представяне,
това съдържание
съответства
на следното
число:
![]()
ПРИМЕР 171. Да се
изпълни
операция
събиране Z=X+Y
на
числата X=10,5 и
Y=99,625, които
са
представени
в разрядна
мрежа с обща
дължина n=12[b]=m+k, където k=4[b] е
дължината на
полето за
представяне
на
характеристиката,
а m=8[b] е
дължината на
полето за
представяне
на мантисата
(без скрития
бит).
Във форма
с плаваща
запетая
числата X и Y
имат вида:
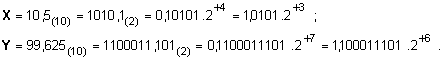
Последният
вид на
числата се
характеризира
с мантиса,
която е
нормализирана
в смисъла на
техниката на скрития
бит.
Характеристиките
на числата са:
![]()
Така
подготвените
за операция
числа имат вида:
![]()
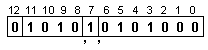
![]()
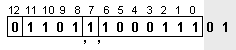
Вижда се,
че значещата
част на
числото Y е
по-дълга от
предвиденото
за мантисата
на числото
поле и двата
младши
разряда ще
бъдат
загубени.
Така числото
ще бъде
изобразено
неточно.
Допусната
грешка е
принципна и не
може да бъде
отстранена. Все
пак трябва да
отбележим, че
ако числото беше
изобразявано
без
прилагане на
техниката на
скрития бит,
то загубена
щеше да се окаже
и цифрата,
стояща в
най-младшия
разряд на
мантисата
(бит №0). Така скритият
бит води до
повишаване
точността на
изчисленията.
Представените
по този начин
числа встъпват
в операция
събиране.
Тъй
като числото X
има по-малка
характеристика
![]()
за
характеристика
на резултата
се приема тази
на числото Y, a в
етапа “изравняване
на
порядъците”,
мантисата на X
се измества
надясно на 3
разрядa и
приема вида:
0,0010101 .
Трябва
да се помни,
че този етап
е също източник
на принципна
грешка. След
това се извършва
събирането:

Получената
сума е
нормализирано
число в смисъла
на скрития
бит, т.е.
![]()
Така
окончателно
от знак,
характеристика
и мантиса се
сглобява
съдържанието
на разрядната
мрежа,
представящо
получената
сума:
![]()
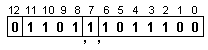
Записаната
в
оперативната
памет на
процесора
сума ще има
следния вид:
![]()
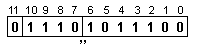
в който
липсва
старшата
единица
(цялата част
на
мантисата).
Според
формата за
представяне,
това съдържание
съответства
на следното
число:
![]()
Полученото
число е
по-малко от
истинската
сума, която е 110,125.
ПРИМЕР 172. Да се
изпълни
операция
събиране Z=X+Y на
числата X=248 и
Y=21, които
са
представени
в разрядна
мрежа с обща
дължина n=12[b]=m+k,
където
k=4[b] е
дължината на
полето за
представяне
на
характеристиката,
а m=8[b] е
дължината на
полето за
представяне
на мантисата
(без скрития
бит).
Във форма
с плаваща
запетая
числата X и Y
имат вида:
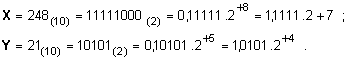
Последният
вид на
числата се
характеризира
с мантиса,
която е
нормализирана
в смисъла на
техниката на
скрития бит.
Характеристиките
на числата са:
![]()
И така,
подготвените
за операция
числа имат
вида:
![]()
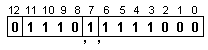
![]()
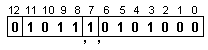
Тъй като
характеристиката
на числото Y е
по-малка от
тази на X, то за
характеристика
на резултата
първоначално
се приема
тази на
числото X:
![]()
Мантисата
на второто
число се
денормализира
чрез
изместване
на 3 разряда надясно,
при което тя
приема вида:
![]() .
.
Представените
по този начин
числа встъпват
в операция
събиране.
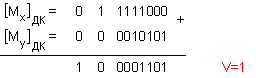
Както
може да се
види от
знаците на
числата, при
извършеното
събиране е
настъпило
положително
препълване.
Ето защо
кодовата
сума не е
допълнителният
код на сумата
от числата.
Получената сума
е число
по-голямо от
числото
![]()
т.е.
то е
ненормализирано
отляво.
Известно е
обаче, че
това
препълване е
с не повече
от един
порядък
(спрямо максимално
възможния) и
лесно може да
бъде отстранено,
ако
получената
сума се
измести надясно
на един бит.
Тогава
мантисата на
резултата ще
получи вида:
![]()
За
да се запази
същото
количество,
към характеристиката
трябва да се
прибави
единица и тя
ще получи
стойността:
![]()
Тази
стойност, за
дефинираната
тук разрядна
мрежа, е
максимално
представимата,
ето защо
полученият
тук резултат е
изключение
и следва да
се отбележи с
признак “NAN”. Той
ще бъде
фиксиран във
вида:
![]()
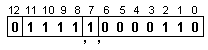
![]()
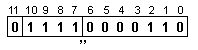
ПРИМЕР 173. Да се
изпълни
операция
изваждане Z=X-Y на
числата X=248 и
Y=21, които
са
представени
в разрядна мрежа
с обща
дължина n=12[b]=m+k,
където k=4[b] е
дължината на
полето за
представяне
на
характеристиката,
а m=8[b] е
дължината на
полето за
представяне
на мантисата
(без скрития
бит).
Този
пример за
операция
изваждане ще
се изпълни с
операндите
от
предидущия
пример, така
че тяхното
представяне
ще приемем за
вече изложено.
Тъй
като
характеристиката
на числото Y е
по-малка от
тази на X, то за
характеристика
на резултата
първоначално
се приема
тази на
числото X:
![]()
Мантисата
на второто
число се
денормализира
чрез
изместване
на 3 разряда
надясно, при
което тя
приема вида:
![]()
Поради
това, че тази
мантиса е
имала 3 младши
нули, след
споменатото
изместване
надясно няма
загуба на
точност.
Представените
по този начин
числа встъпват
в операция
изваждане:
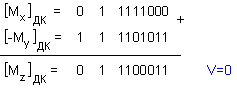
Полученият
резултат е
положително
число, нормализирано
в смисъла на
скрития бит,
ето защо може
веднага да се
сглоби
окончателният
вид на
резултата:
![]()
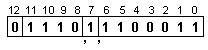
Според
формата за
представяне,
това
съдържание
съответства
на следното
число:
![]()
ПРИМЕР 174. Да се
изпълни
операция
изваждане Z=X-Y на
числата X=496 и
Y=-51, които
са
представени
в разрядна мрежа
с обща
дължина n=12[b]=m+k,
където k=4[b] е
дължината на
полето за
представяне
на
характеристиката,
а m=8[b] е
дължината на
полето за
представяне
на мантисата
(без скрития
бит).
Във форма
с плаваща
запетая
числата X и Y
имат вида:
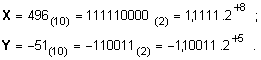
Характеристиките
на числата
са:
![]()
И така,
подготвените
за операция
числа имат
вида:
![]()
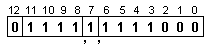
![]()
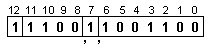
Тъй като
характеристиката
на числото Y
е по-малка от
тази на X, то
за
характеристика
на резултата
първоначално
се приема
тази на
числото X:
![]()
Мантисата
на второто
число се
денормализира
чрез
изместване
на 15-12=3 разряда
надясно, при
което тя
приема вида:
![]()
Тази
мантиса губи
младшата
единица от
значещата си
част и
участва в
операцията
със загуба на
точност.
Представените
по този начин
числа встъпват
в операция
изваждане:
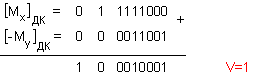
Получената
кодова сума
не е
допълнителният
код на сумата
от числата
тъй като е
настъпило
положително
препълване. Това
препълване
обаче е с не
повече от
един порядък,
така че
резултатът
може да се
нормализира
като се
измести
надясно на
един бит.
Тогава
мантисата на
резултата ще
добие вида
![]()
Неточността
на мантисата
при това се
засилва,тъй
като тя губи
най-младшата
си единица.
Нормализацията
на мантисата
на резултата
води до
корекция на
характеристиката,
чиято
временна
стойност се
съхранява в
брояча на
характеристиката:
(БрН)=(БрН)+1=15+1=16.
Тази стойност
обаче
препълва
основното
поле на този
брояч
(младшите му 4
разряда, т.е.
(БрН)=1 0000; V=1). Това е препълване
в полето на
характеристиката.
Полученият
резултат е
неверен и за
дефинираната
тук разрядна
мрежа това
означава, че
е настъпило
окончателно “препълване
при плаваща
запетая”.
ПРИМЕР 175.
Да се
изпълни
операция
изваждане Z=X-Y на
числата X=0,11001.2-6 и Y=0,10101.2-4,
които са
представени
в разрядна мрежа
с обща
дължина n=12[b]=m+k,
където k=4[b] е
дължината на
полето за
представяне на
характеристиката, а
m=8[b] е
дължината на
полето за
представяне
на мантисата
(без скрития
бит).
Във
форма с
плаваща
запетая и
скрит бит числата
X и Y
получават
вида:
![]()
Характеристиките
на числата
са:
![]()
И
така,
подготвените
за операция
числа имат
вида:
![]()
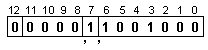
![]()
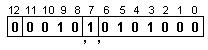
Тъй
като
характеристиката
на числото X е
по-малка от
тази на Y, то за
характеристика
на резултата
първоначално
се приема
тази на числото
Y:
![]()
Мантисата
на първото
число се
денормализира
чрез
изместване
на 2 разряда
надясно, при
което тя
приема вида:
![]() .
.
Представените
по този начин
числа встъпват
в операция
събиране.
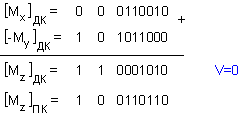
Получената
сума от двете
мантиси е
отрицателно
число, което
не е
нормализирано
в смисъла на
скрития бит.
За да се
нормализира,
получената
сума трябва
да се измести
наляво на два
разряда.
Тогава
мантисата ще
има вида:
![]()
а от
предварителната
стойност на
характеристиката
на резултата
ще бъдат
извадени две
единици:
![]()
Полученият
в разрядната
мрежа
резултат има
следния вид:
![]()
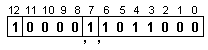
Получената
ситуация се
отнася към
изключителните.
Според
теоретичните
определения,
представени
в книга [1],
полученият
резултат се
признава за
равен на
числото “машинна
нула”,
независимо
от
стойността
на скрития
бит. Така
окончателният
резултат ще бъде:
![]()
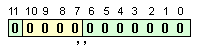
Ако
обаче АЛУ е
инициализирано
за работа в режим
на недостиг,
то
първоначалният
вид на
резултата ще
бъде запазен
– той ще има
вида:
![]()
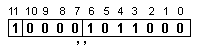
и
тогава ще
говорим, че
числото Z е
съхранено в
паметта “с
ниво на
недостиг
нула”. В още
по-тежките
случаи,
когато
стойността нула
в полето на
характеристиката
се достига
преди
мантисата на
резултата да
се нормализира,
същият може
да се съхрани
с ниво на недостиг
по-голямо от
нула. С това
следващите
изчислителни
резултати, в
които той ще
участвува, ще
бъдат
значително
по-точни.
ПРИМЕР 176.
Да се
изпълни
операция
умножение Z=X.Y на
числата
X = 0,110101.2+2 = 3,3125
и Y = -0,101101.2-2 = -0,17578125 ,
които
са
представени
в разрядна
мрежа с обща
дължина n=12[b]=m+k,
където k=4[b] е
дължината на
полето за
представяне
на
характеристиката,
а m=8[b] е
дължината на
полето за
представяне
на мантисата.
Произведението
от тези две
числа е
Z
≈ -0,582275390625.
Във
форма с
плаваща
запетая и
скрит бит числата
X и Y
получават
вида:
![]()
Характеристиките
са:
![]()
И
така,
подготвените
за операция
числа имат
вида:
![]()
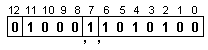
![]()
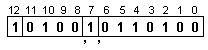
Характеристиките
на числата се
събират по
следния
начин:
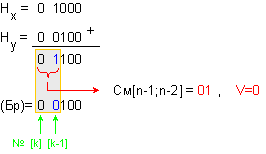
Събирането
на
характеристиките
е без препълване
и получената
временна
сума се записва
в брояча на
характеристиката.

Получената
мантиса:
![]()
е число
с двойна
дължина.
Освен това то
е ненормализирано,
което налага
неговото изместване
надясно на
един бит.
Така
мантисата
![]()
става
нормализирана
по стандарта
със скрит бит
и след
отрязване на
младшите й
цифри тя може
да се запише
с единична
дължина в
разрядната
мрежа, т.е.
![]()
Нормализацията
на
произведението
изисква
прибавяне на
една единица
към характеристиката
на резултата,
което се
извършва в
брояча на
характеристиките
и тя получава
стойността
![]()
Тази
характеристика
обаче не е вярна!
Неверният
резултат се
дължи на
принципна грешка
в сумата от
характеристиките:
![]()
Както
може да се
види от
получения
по-горе израз,
характеристиката
на
произведението
съдържа един
път в повече
отместването
{D-1}. Тъй като
отнемането
на основната
му съставяща
D се
реализира в
процеса на
запис в брояча
на
характеристиката
автоматично,
остава да се
добави една
единица,
отнета в
повече. В
примера тук
това ще
направим
сега:
![]()
Така
всички
елементи на
структурата
на разрядната
мрежа са
получени и
произведението
може да бъде
сглобено
окончателно:
![]()
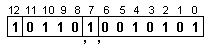
Изобразеното
съдържание
представлява
числото:
![]()
Както
може да се
види,
резултатът е
по-малък от
истинската
стойност,
което се
дължи на загубата
на точност в
отделните
етапи на алгоритъма
и зададения
формат на
разрядната
мрежа.
ПРИМЕР 177.
Да се
изпълни
операция
деление Z=X/Y на
числата X=0,1101.2+4 и Y=-0,1011.2+2,
които са
представени
в разрядна мрежа
с обща
дължина n=12[b]=m+k,
където k=4[b] е
дължината на
полето за
представяне
на характеристиката,
а m=8[b] е
дължината на
полето за
представяне
на мантисата.
Във
форма с
плаваща
запетая и
скрит бит числата
X и Y се
записват
както следва:
![]()
Частното
е числото
Z = X/Y =
-4,72727272727272727272727272727273 .
То е неточно
представено,
защото 16-тата
двойка повтарящи
се цифри (72) е
закръглена
на 73. Характеристиките
на числата
са:
![]()
И
така,
подготвените
за операция
числа имат
вида:
![]()
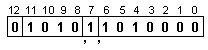
![]()
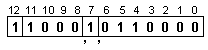
Характеристиките
на числата се
изваждат по
следния
начин:
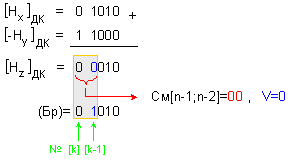
При
това
изваждане
няма
препълване и
тригерът на
препълването
остава в
състояние нула
(ТП=0). Така
получената
на изхода на
суматора
сума се
коригира
автоматично
при
записването
си в брояча
на характеристиката.
Броячът
приема
стойността (БрН)=0 1010,
където в
неговия
най-старши
разряд се
записва нула,
а в [k-1]–я
следното:
![]()
Тази
все още
неокончателна
характеристика
на частното,
която апаратурата
получава, не е
вярна! От
една страна
неверният
резултат се
дължи на
принципната
грешка в
разликата на
характеристиките:
![]()
която е
равна на
порядъка на
частното. От
друга страна
извършената
вече
автоматична
корекция при
записа на
разликата в
брояча на
характеристиката
представлява
сумата
![]()
който в
смисъла на
скрития бит е
също неверен,
тъй като
съдържа една
единица в
повече. Необходимият
ни верен
резултат
трябва да има
стойността
![]()
който
може да се
получи от
наличната в
брояча
стойност
чрез
отнемане на
една единица:
![]()
След
първоначалното
изваждане и
коригиране
на
характеристиките
следва
делението на
двете
мантиси. Тук
то е
извършено по
метода без
възстановяване
на
остатъците
по схемата с
неподвижен
делител по
модул:
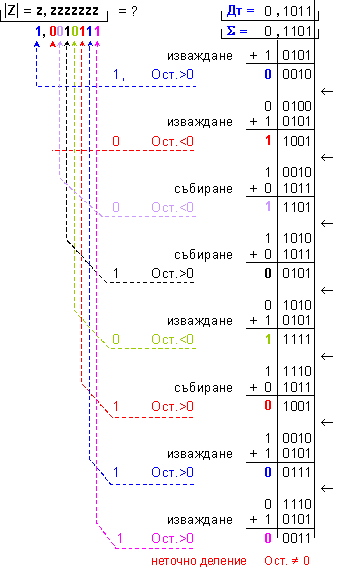
Полученото
частно
![]()
е число
по-голямо от
единица и
следователно
се приема за
нормализирано
в смисъла на
скрития бит.
Така
окончателно
от знак,
характеристика
и мантиса в
разрядната
мрежа се
сглобява резултатът:
![]()
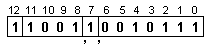
Това
съдържание
представя
числото:
![]()
Този
резултат се
различава от
по-точния,
който е -4,72(72).
Това се дължи
в случая на неточното
деление.
Следващият
раздел е:
6.
Преобразуване
на формите и
на форматите
на числата