VI.
ПРЕОБРАЗУВАНЕ
НА ФОРМИТЕ И
НА ФОРМАТИТЕ
НА ЧИСЛАТА
VI.1
Преобразуване
на двоични
числа с дясно
фиксирана
запетая в
двоични с
плаваща
запетая
Както
за всеки
раздел на
тази книга,
така и в този,
отново
следва да
предупредим
читателя, че
числените
примери
по-долу могат
да му бъдат
полезни, само
ако преди
това се е
запознал с
теоретичните
постановки,
които те илюстрират,
а те за тук
разглежданата
тема са представени
в раздел 3.7
на книга [1].
Алгоритмите
за
преобразуване
на формата, в
която са
представени
числата (ФЗ→ПЗ, ПЗ→ФЗ),
предполагат
една и съща
дължина на
разрядната
мрежа както
за фиксирана
запетая, така
и за плаваща
запетая.
Когато
дадено число
с фиксирана
запетая се
представя в
разрядна
мрежа с
дължина n[b],
порядъкът му
се определя
по формулата
p = (n-1) - L ,
където с L е означен броят на изместванията на числото в разрядната мрежа при неговата лява нормализация. Числото L е число със знак, тъй като изместванията са възможни в посока както наляво, така и надясно. Случаят с изместване надясно се отнася единствено за най-малкото число, представимо в допълнителен код в разрядната мрежа с фиксирана запетая, т.е. за Xmin . Изчислението на порядъка се изпълнява апаратно в брояча на характеристиките. Началната стойност в този брояч се установява автоматично БрН:=(n-1). Тъй като се работи в стандарта с изместен порядък, т.е. с характеристиката, началната стойност следва да бъде БрН:=D+(n-1). Тогава характеристиката се изчислява така
H
= D+(n-1) - L ,
Известно е, че:
·
Всяко число с
фиксирана
запетая е
представимо
във форма с
плаваща
запетая.
·
Всяко число с
фиксирана
запетая,
чийто модул
има дължина
по-малка от
дължината на
полето,
определено
за мантисата,
се
представя
точно.
·
Всяко число с
фиксирана
запетая,
чийто модул
има дължина
по-голяма от
дължината на полето,
определено
за мантисата,
се
представя
неточно.
Числените
примери,
представени
в този раздел,
илюстрират
формата с
плаваща
запетая в
стандарта с
изместен
порядък, но
без техниката
на скрития
бит. Следва
да се
припомни, че
мантисата се
представя в
прав код.
ПРИМЕР 178. Да се
представи
цялото
число X=79
във форма с
плаваща
запетая в
разрядна
мрежа с обща
дължина n=16[b]=m+k,
където k=6[b] е
дължината на
полето за представяне
на
характеристиката,
а m=10[b] е
дължината на
полето за
представяне
на мантисата.
Двоичният
еквивалент
на даденото
число е
![]()
В
разрядната
мрежа с
фиксирана
запетая в допълнителен
код числото
има вида:
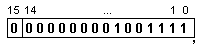
Характеристиката
на числото
![]()
с
плаваща
запетая се
получава
последователно
в брояча на
характеристиките,
в резултат на
лявата
нормализация
на горното
съдържание:

Така
всички
елементи на
структурата
стават
известни и
може да се
сглоби следното
съдържание
на
разрядната
мрежа:
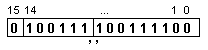
което
съответства
на следното
число:
![]()
ПРИМЕР 179. Да се
представи
цялото
число X=5711 във форма с
плаваща
запетая в разрядна
мрежа с обща
дължина n=16[b]=m+k,
където k=6[b] е
дължината на
полето за
представяне
на
характеристиката,
а m=10[b] е
дължината на
полето за
представяне
на мантисата.
Двоичният
еквивалент
на даденото
число е
![]()
В разрядната
мрежа с
фиксирана
запетая в
допълнителен
код числото
има вида:
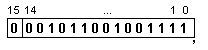
Характеристиката
на числото
![]()
с
плаваща
запетая се
получава
последователно
в брояча на
характеристиките,
в резултат на
лявата
нормализация
на горното
съдържание:
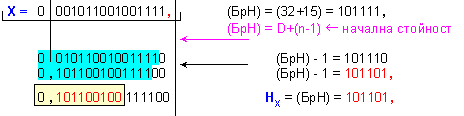
Така
всички
елементи на
структурата
стават
известни и
може да се
сглоби
следното съдържание
на
разрядната
мрежа:
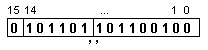
което
съответства
на следното
число:
![]()
Както
се вижда след
направената
проверка, представеното
с плаваща
запетая в
зададения
формат на
разрядната
мрежа число 5696 не е равно
на
зададеното.
То е с 15
единици
по-малко!
Това се дължи
на факта, че
модулът на
цялото число
е по-дълъг от отредената
дължина за
мантисата (m-1)
бита.
Така
изходната
последователност
от двоични
цифри е
загубила 4
младши
единици, които
формират
стойността
на загубата,
т.е. на
грешката,
която е равна
на 15, (5696=5711-15).
Така този
пример
илюстрира
възможната
неточност
при
преобразуване
цели числа в
реални, ето
защо
програмистът
носи
отговорността
за
правилното
деклариране
на типовете
на съответните
променливи.
ПРИМЕР 180. Да се
представи
цялото
число X=-79 във
форма с
плаваща
запетая в
разрядна
мрежа с обща
дължина n=16[b]=m+k,
където k=6[b] е
дължината на
полето за
представяне
на
характеристиката,
а m=10[b] е
дължината на
полето за
представяне
на мантисата.
Двоичният
еквивалент
на даденото
число е
![]()
В
разрядната
мрежа с
фиксирана запетая
в
допълнителен
код числото
има вида:
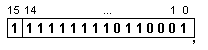
Преди да
започне
изчислението
на характеристиката,
цялото число
трябва да се
преобразува
в прав код,
което не се
прави
единствено в
случая,
когато се
установи, че
в разрядната
мрежа се
намира
числото Xmin.
Тъй като
даденото в
примера
число не е
най-малкото,
то неговият
прав код ще
има вида
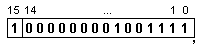
Характеристиката
на числото
![]()
с
плаваща
запетая се
получава
последователно
в брояча на
характеристиките,
в резултат на
лявата
нормализация
на горното
съдържание:
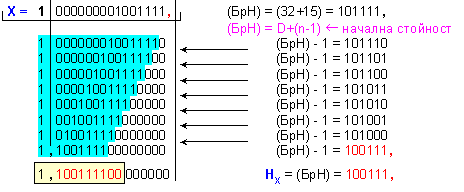
Така
всички
елементи на
структурата
стават
известни и
може да се
сглоби
следното съдържание
на
разрядната
мрежа:
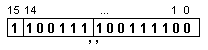
което
съответства
на следното
число:
![]()
Ако
сравним
новото
съдържание
на разрядната
мрежа с това
от
предходния
пример, където
числото има
същия модул,
то ще видим,
че разликата
е само в
най-левия
бит, където
цифрата 1
изразява
знака минус.
ПРИМЕР 181. Да се
представи
цялото
число X=-32768 във форма с
плаваща
запетая в
разрядна
мрежа с обща
дължина n=16[b]=m+k,
където k=6[b] е
дължината на
полето за
представяне
на
характеристиката,
а m=10[b] е
дължината на
полето за
представяне
на мантисата.
Двоичният
еквивалент
на даденото
число (16 битово)
е
![]()
Числото е Xmin
за тази
дължина на
разрядната
мрежа. В
разрядната
мрежа с
фиксирана
запетая в допълнителен
код числото
има вида:
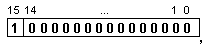
Характеристиката
на числото
![]()
с
плаваща
запетая
следва да се
получи автоматично
в брояча на
характеристиките,
в резултат на
лявата
нормализация
на горното съдържание,
но такава не
може да се
изпълни, тъй
като то се
разпознава
като Xmin.
Единствено в
този случай,
за постигане
на
правилната мантиса
(при това в
прав код) се
изпълнява изместване
надясно,
както
показва
примерът:
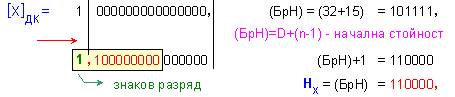
Както
може да се
види в този
пример, “изключителното”
число Xmin в
допълнителен
код, отново прави
изключение
от общото
правило. За
неговата
лява
нормализация
се изпълнява
изместване
надясно, а в
брояча на
характеристиката
се прибавя
единица.
Така
всички
елементи на
структурата
стават
известни и
може да се
сглоби
следното съдържание
на
разрядната мрежа
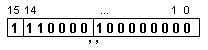
което
съответства
на следното
число:
![]()
ПРИМЕР 182. Да се
представи
цялото
число X=0
във форма с
плаваща
запетая в
разрядна
мрежа с обща
дължина n=16[b]=m+k,
където k=6[b] е
дължината на
полето за
представяне
на
характеристиката,
а m=10[b] е
дължината на
полето за
представяне
на мантисата.
В
разрядната
мрежа с
фиксирана
запетая в допълнителен
код числото
има вида:
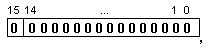
Това
число е също изключение.
Неговата
лява нормализация
е невъзможна,
ето защо за
резултат се
приема
числото “машинна
нула”.
Следващият
раздел е:
6.2
Преобразуване
на двоични
числа с плаваща
запетая в
двоични числа
с дясно
фиксирана
запетая