Последната редакция на тази книга е от 2021 година.

VI.2 Преобразуване на двоични числа с плаваща запетая в двоични числа с дясно фиксирана запетая

Това преобразование, обратно на представеното в предидущия пункт, има повече особености, които ще бъдат илюстрирани тук. Веднага ще бъде отбелязано, че тук се има предвид формата с плаваща запетая без техниката на скрит бит, която не променя по същество алгоритъма на операцията. Авторът е уверен, че читателят би се справил с конкретиката, уповавайки се на теоретичните пояснения, изложени в раздел 3.7 на книга [1], както и на представените по-долу тук числени примери.

Отново следва да предупредим читателя, че числените примери по-долу могат да му бъдат полезни, само ако преди това се е запознал с теоретичните постановки.

· Всяко число с фиксирана запетая следва да бъде точно, тъй като по същество представлява цялата част на реалното число, зададено във форма с плаваща запетая.

· На първо място следва да се посочи фактът, че при отрицателни стойности на порядъците, числото с фиксирана запетая има нулева цяла част, или с други думи, когато порядъкът на числото с плаваща запетая е отрицателен, за резултат се приема числото нула;

· При нулев порядък във формата с плаваща запетая за резултат също се приема числото нула;

· При положителни порядъци във формата с плаваща запетая, числото с фиксирана запетая има фактическа цяла част, която е различна от нула. В този случай тази цяла част е обект на алгоритъма на разглежданото по-долу преобразование и е крайният резултат. По същество това преобразование се изразява в такова изместване на значещата част на числото спрямо дясно фиксираната запетая, при което тя постига точното си съответствие на количеството, което означава. Броят на изместванията L е решение на уравнението

Числото L е число със знак и ако последният е плюс, изместванията са надясно, ако е минус – наляво.

ПРИМЕР 183. Да се преобразува даденото във форма с плаваща запетая в разрядна мрежа с обща дължина n=16[b]=m+k число X:

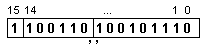
във форма с фиксирана запетая. Дължината на полето за представяне на характеристиката е k=6[b], а дължината на полето за представяне на мантисата е m=10[b].

Зададеното съдържание на разрядната мрежа с плаваща запетая съответства на числото:

а началното съдържание на брояча на характеристиката, при така определената в примера разрядна мрежа, е

Преобразованието започва с изваждане на съдържанието на полето на характеристиката от началното съдържание на брояча на характеристиката:

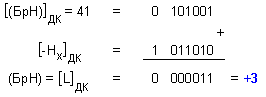
Съдържанието на брояча на характеристиката е положително число, ето защо мантисата, която все още стои в разрядната мрежа, се измества надясно, докато броячът се нулира:

Полученото съдържание на разрядната мрежа може да се интерпретира като числото Х=-37.

Както се вижда, цялата стойност на числото е загубила 0,75 единици, което се дължи на отпадане на 3 младши цифри на мантисата.

ПРИМЕР 184. Да се преобразува даденото във форма с плаваща запетая в разрядна мрежа с обща дължина n=16[b]=m+k число X:

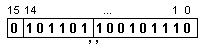
във форма с фиксирана запетая. Дължината на полето за представяне на характеристиката е k=6[b], а дължината на полето за представяне на мантисата е m=10[b].

Зададеното съдържание на разрядната мрежа с плаваща запетая съответства на числото:

Началното съдържание на брояча на характеристиката, при така определената в примера разрядна мрежа, е

Преобразованието започва с изваждане на съдържанието на полето на характеристиката от началното съдържание на брояча на характеристиката:

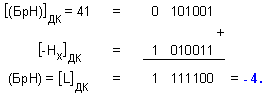
Съдържанието на брояча на характеристиката е отрицателно число, представено в допълнителен код, ето защо мантисата, която все още стои в разрядната мрежа, се измества наляво, докато броячът се нулира:

Получената последователност е цяло число в прав код. Неговата стойност е Х=4832.

ПРИМЕР 185. Да се преобразува даденото във форма с плаваща запетая в разрядна мрежа с обща дължина n=16[b]=m+k число X:

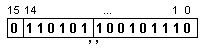
във форма с фиксирана запетая. Дължината на полето за представяне на характеристиката е k=6[b], а дължината на полето за представяне на мантисата е m=10[b].

Зададеното съдържание на разрядната мрежа с плаваща запетая съответства на числото:

Началното съдържание на брояча на характеристиката, при така определената в примера разрядна мрежа, е

Преобразованието започва с изваждане на съдържанието на полето на характеристиката от началното съдържание на брояча на характеристиката:

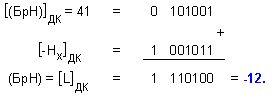
Съдържанието на брояча на характеристиката е отрицателно число, представено в допълнителен код, ето защо мантисата, която все още стои в разрядната мрежа, се измества наляво, докато броячът се нулира:

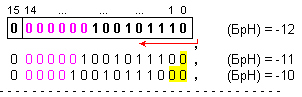
Ясно се вижда, че старшите цифри на числото ще излязат извън левия край на разрядната мрежа далече преди броячът на характеристиката да се нулира. Така, в следствие на твърде високия порядък на числото (21>>15), настъпва препълване на разрядната мрежа с фиксирана запетая. Този случай може да се разпознава предварително по получаваната в брояча разлика. Ако съдържанието на брояча удовлетворява неравенството (БрН) < -6 = (-k) , то автоматично може да се генерира препълване. Разпознаването може да се реализира и преди изваждането на характеристиката, ако се реализира дешифриране на нейните стойности:

Тази ситуация се дължи на факта, че диапазонът на представимите във форма с плаваща запетая числа, е много по-голям от този на числата с фиксирана запетая.

ПРИМЕР 186. Да се преобразува даденото във форма с плаваща запетая в разрядна мрежа с обща дължина n=16[b]=m+k число X:

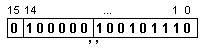
във форма с фиксирана запетая. Дължината на полето за представяне на характеристиката е k=6[b], а дължината на полето за представяне на мантисата е m=10[b].

Зададеното съдържание на разрядната мрежа с плаваща запетая съответства на числото:

Преобразуването започва с изваждане на съдържанието на полето на характеристиката от началното съдържание на брояча на характеристиката:

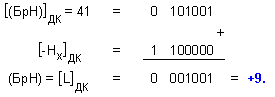
Съдържанието на брояча на характеристиката е положително число, представено в допълнителен код, ето защо мантисата, която все още стои в разрядната мрежа, се измества надясно, докато броячът се нулира. В този пример изместванията са 9, точно колкото е дължината на полето на мантисата, което означава, че след тези измествания последната ще се окаже извън него. Така за резултат ще се получи число нула.

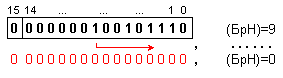
Този случай може да се разпознава предварително по получаваната в брояча разлика. Ако съдържанието на брояча удовлетворява неравенството (БрН) > 9=(m-1) , то без да се извършват измествания за резултат може да се установи число нула. Разпознаването може да се реализира и преди изваждането на характеристиката, ако се реализира дешифриране на нейните стойности:

Зададеното в примера число е гранично със своя порядък.

Интерес представлява случаят, когато е зададено отрицателно число със същия порядък, например зададеното в този пример число, но със знак минус:

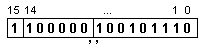
След изваждане на характеристиката отново ще се получи разликата (БрН)=+9, което означава, че ако се извършат 9 измествания на мантисата надясно ще се получи съдържанието:

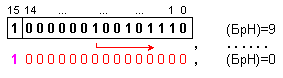
което съответства на допълнителния код на най-малкото число в разрядната мрежа с фиксирана запетая. В същото време истинският резултат е числото нула. Ето защо, за да се гарантира крайният резултат, в случаите, когато получената в брояча разлика е (БрН) ³ 9, алгоритъмът следва да завършва с нулиране на разрядната мрежа.

Следващият раздел е:

6.3 Преобразуване на форматите на числата