Последната редакция на тази книга е от 2021 година.

VI.3 Преобразуване на форматите на числата

Следва веднага да кажем, че под формат разбираме дължината на разрядната мрежа, както и тази на отделните й структурни полета. Възможностите за промяна на формата, в който е изобразено дадено число, са две – скъсяване и удължаване. И в двата случая това е възможно само в рамката на хардуерната организация на разрядната мрежа. Последната е невъзможно да бъде променяна с програмни средства. Различните формати на данните са организирани апаратно на микрооперационно ниво и се подразбират в алгоритмите на отделните машинни команди. Именно тези формати определят възможностите в езиците за програмиране да декларират определен тип променливи.

Преобразованията на форматите се осъществяват от специално създадени машинни команди.

ПРИМЕР 186. ЧИСЛА С ФИКСИРАНА ЗАПЕТАЯ

Скъсяване на формата на число, представено във форма с фиксирана запетая, не се практикува. За такова преобразование няма машинни команди. Причина за това е възможността за допускане на груби грешки в стойността на числото.

Например, ако е дадено 16-битовото число

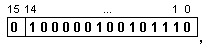
неговото скъсяване до 8-битовия формат изисква премахване на старшия байт и пренасяне на знаковия бит в останалата част. Така би се получило следното

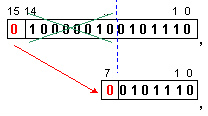
Полученият резултат не се нуждае от коментар.

Удължаването на формата на числа с ФЗ е възможно и се практикува чрез машинни команди от типа Convert Byte (Word) to Word (Doubleword) . Преобразованието се свежда до двойно удължаване на изходния формат с добавяне отляво, т.е. в старшата половина, на така нареченото “знаково удължение”, което е подробно изяснено в книга [1]. Ще илюстрираме графично това така

Положително число в допълнителен код Отрицателно число в допълнителен код

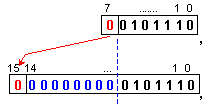
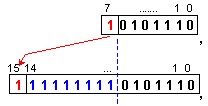
Ще припомним, че в допълнителен код незначещата цифра съвпада със знаковата, затова допълнената дължина се запълва с нули или с единици.

ПРИМЕР 187. ЧИСЛА С ПЛАВАЩА ЗАПЕТАЯ

Форматите за числата с плаваща запетая традиционно са три – с единична, с двойна и с разширена точност. Ще припомним, че разрядната мрежа, която е апаратно реализирана в устройството за работа с плаваща запетая (FPU), е 80 битова. Това се нарича още “вътрешен формат”. Преобразованията на форматите се налагат в два случая:

· При зареждане на операнд във входен регистър на FPU;

· И обратно, при запомняне на резултат, получен в FPU, в паметта, в съответния формат MemF, заявен от програмиста.

Запомнените в паметта стойности имат структурата MemF:(S,H,M). Тези формати бяха означени като SP (единична точност) и DP (двойна точност). След прочитане на операнд от паметта той следва да се зареди във входен регистър на устройството за работа с плаваща запетая, при което трябва да се преобразува до пълния вътрешен формат от 80 бита (1+15+64). Като се имат предвид дължините на изходния формат SP от 32 бита (1+8+23) или на DP от 64 бита (1+11+52), става ясно, че както характеристиката Н, така и мантисата М, трябва да бъдат представени в полета с по-голяма дължина, а към мантисата още трябва да се конкатенира старша единица, стойност на скрития бит. Постигането на вътрешния формат на мантисата е лесно. Тъй като тя е число с ляво фиксирана запетая, удължаването й е отдясно чрез добавяне на необходимия брой незначещи нули.

Например, ако изходният вид на мантисата е:

,bbbb … bbb - комбинация с дължина 23 или 52 бита

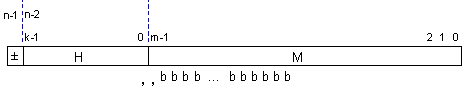
за вътрешния формат получаваме:

1,bbbb … bbb000 ... 000 - комбинация с дължина 64 бита (1+63),

който както се вижда, е получен след добавяне отдясно на съответния брой нули.

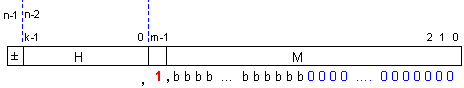
Характеристиката Н е цяло число, т.е. число с дясно фиксирана запетая. Стойността на това число се определя от формулата

H = p+(D-1) = (p-1)+D .

От своя страна стойността на отместването D е равна на теглото на старшия бит в полето на характеристиката, т.е. D=2⁷ или D=2¹⁰ или D=2¹⁴ за съответните формати. Ако стойността (p-1) е положително число, видът на характеристиката може да бъде:

100...00bb…bb, - комбинация с дължина 8 или 11 бита.

Ако модулът на порядъка е достатъчно голям, е възможно комбинацията да има следния вид:

1bbb…bbb…bb, - комбинация с дължина 8 или 11 бита.

За да стане тази комбинация характеристика във вътрешния формат от 15 бита, след старшата единица се вмъкват (добавят) липсващите незначещи цифри нула (0):

100...0000...00bb…bb, - комбинация с дължина 15 бита, или

100...00bbb…bbb…bb, - комбинация с дължина 15 бита.

Добавеното поле (Supplement) има известна дължина, която ще означим с буква S. Дължината на това поле може да се изчисли както следва

където от дължината на полето за характеристика L_ЕР на вътрешния формат (15 бита) се изважда дължината на същото поле в по-късите формати (8 или 11 бита). Така дължината S на добавеното поле може да бъде 7 или 4 бита съответно.

Ако стойността (p-1) е отрицателно число, видът на характеристиката е:

011...11bb…bb, - комбинация с дължина 8 или 11 бита.

Ако модулът на порядъка е достатъчно голям, е възможно комбинацията да има следния вид:

0bbb…bbb…bb, - комбинация с дължина 8 или 11 бита.

За да стане тази комбинация характеристика във вътрешния формат от 15 бита, след старшата нула се вмъкват липсващите незначещи цифри единица (1):

011...1111...11bb…bb, - комбинация с дължина 15 бита, или

011...11bbb...bbb…bb, - комбинация с дължина 15 бита.

Преобразования не се изпълняват, когато числото пристига в устройството с формат EF, който съвпада с вътрешния, т.е. 80 бита или 10 байта.

Вторият вид преобразования (скъсяване) се изпълняват, когато изчисленият в FPU резултат трябва да се запомни в паметта, където ще се съхранява в заявения от програмиста MemF. Не се извършват преобразования ако резултатът се запомня във формата, в който е получен (10 байта). В останалите случаи се налага скъсяване. Аналогично на преобразованията, описани по-горе, и тук се налага да се изяснят действията, свързани с двата основни елемента на структурата – характеристика и мантиса.

Характеристиката е цяло число, записано в поле с дължина 15 бита. Пренасянето на това число в поле с дължина 8 или 11 бита изисква скъсяване на изображението отляво. Но ако значещата част на съдържащия се в изображението порядък е достатъчно дълга, то той няма да може да се изобрази в по-късия формат. Така възниква въпросът - как да се разпознава тази ситуация? Ще приемем първоначално, че характеристиката изобразява положителен порядък, което пък означава, че най-старшият й бит е единица. Ако вдясно от тази единица съществува група от поне S на брой нули (0), то комбинацията има следния вид:

100...00bbb…bbb…bb, - комбинация с дължина 15 бита.

Отнемането на тази група от S на брой нули ще даде характеристиката в желания формат и тя ще има вида:

1bbb…bbb…bb, - комбинация с дължина 8 или 11 бита.

Ако обаче вдясно от старшата единица на характеристиката не съществуват S на брой последователни нули, това означава, че изобразеният порядък е по-голям от максимално възможния за потребителския формат на характеристиката. Това за преобразованието означава препълване на разрядната мрежа с искания по-къс формат.

Ако най-старшата цифра на характеристиката е нула, това означава, че изобразеният порядък е отрицателно число. Ако вдясно от тази нула съществува група от поне S на брой единици (1), то комбинацията има следния вид:

011...11bbb...bbb…bb, - комбинация с дължина 15 бита.

Отнемането на тази група от S на брой единици ще даде характеристиката в желания формат и тя ще има вида:

0bbb...bbb…bb, - комбинация с дължина 8 или 11 бита.

Ако обаче вдясно от старшата нула на характеристиката не съществуват S на брой последователни единици, това означава, че модулът изобразения порядък е по-голям от максимално възможния за потребителския формат на характеристиката. Това за преобразованието означава силно отрицателно препълване на разрядната мрежа с искания по-къс формат. Нормално е в този случай резултатът в по-късия формат на се замести с машинната нула.

И на края остана да изясним как се скъсява мантисата, което след всичко казано до тук, не е така неясно. Мантисата губи старшата си единица (скрития бит) и бива отрязана отдясно със съответния брой битове, така че от 63 да останат 23 или 52. С цел по-малка грешка е възможно да се изпълни закръгляне до младшия бит на формата MemF, в който се съхранява числото.

Следващият раздел е:

7. Изчисляване на елементарни функции