VII.
ИЗЧИСЛЯВАНЕ НА ЕЛЕМЕНТАРНИ
ФУНКЦИИ
В
съвременни
условия,
благодарение
на възможностите
на
микроелектронните
технологии, в
цифровите
процесори е
вградено изчисляването
на някои
елементарни
функции в
качеството
им на изпълними
операции. В
повечето
случаи това
са функции от
един аргумент.
Алгоритмите
за
изчисляване
на тези
функции са
твърде
различни и
достатъчно
сложни.
Синтезът на
логически
структури на
устройства
за тяхната
реализация е
задача, с
която няма да
се
занимаваме
тук. Тук поставената
тема ще бъде
само
илюстрирана
чрез
алгоритъма
за
изчисляване
на функцията 
. Операция
извличане на
корен втори
най-удобно се
алгоритмизира
за числа с
ляво фиксирана
запетая.
Анализът на
функцията,
синтезът на
алгоритъма
за нейното
изчисление,
както и
синтезът на
логическата
структура на
устройството
за неговата
реализация,
читателят
може да намери
в книга [1],
пункт 3.9.1. При
изпълнение
на примерите
се има предвид
модулът на
подкоренната
величина.
Численият
пример
представлява
рисунка,
чиято
структура
съответства
на
логическата
структура на
синтезираното
устройство.
По тази
причина
читателят следва
добре да го
познава и
тъкмо за това
ще му помогне
и самият
числен
пример.
ПРИМЕР 188.
Да се
изчисли
функцията 
, за
стойността
на аргумента X=0,390625 , при
дължина на
разрядната
мрежа n=6[b].
Двоичният
еквивалент
на
зададеното
число е:
|X|=0,011001
.
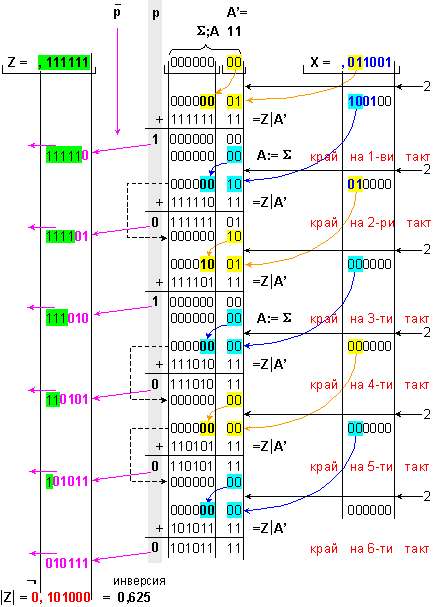
Забележка:
Стрелките с
пунктир в
примера
показват, че
когато липсва
пренос при
събиране,
съдържанието
на РгА
не се
променя, тъй
като не се
извършва
обратен
запис на
получената
сума (вижте
логическата
структура от фигура 3.9.1.1,
книга [1]).
ПРИМЕР 189.
Да се
изчисли
функцията 
, за
стойността
на
аргумента X=0,47265625
, при
дължина на
разрядната
мрежа n=8[b].
Числото
X
е получено от
отношението X=121/256 и
двоичният му
еквивалент
е: |X| = 0,01111001.
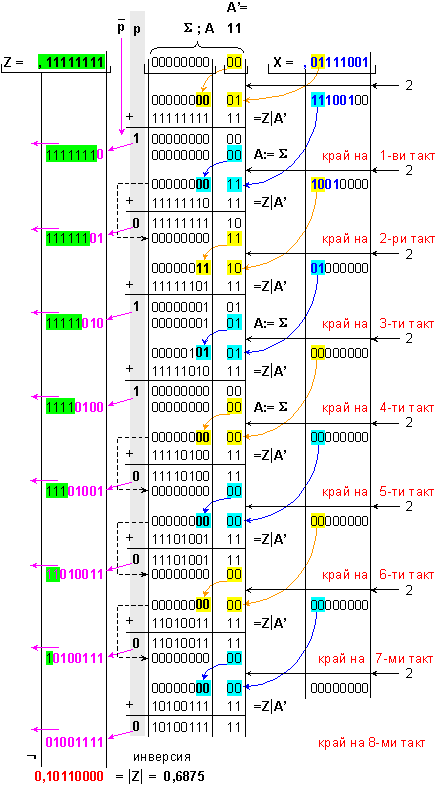
ПРИМЕР 190.
Да се
изчисли
функцията 
, за
стойността
на
аргумента X=121
, при
дължина на
разрядната
мрежа n=8[b].
Числото
X е цяло
число (с
дясно
фиксирана
запетая) и
двоичният му еквивалент
е:
|X| = 1111001,0
.
Ако
подкоренната
величина X
е зададена
като число с
дясно
фиксирана запетая,
т.е. цяло
число, то
изчисляването
на стойността
на функцията 
може да се
извърши
според
следната формула:
ако числото
преди това се
представи
във форма
с плаваща
запетая.
Вероятно
на читателя
вече е ясно,
че представеният
по-горе
алгоритъм в
този случай
се прилага
върху
мантисата на
числото,
която представлява
число с ляво
фиксирана
запетая.
Известно
затруднение
може да
създаде порядъкът,
ако е нечетно
число. Изход
от такава
ситуация е
предварителното
денормализиране
на мантисата
чрез изместване
на един бит
надясно и
прибавяне на
единица към
порядъка, с
което той
става четно
число.
И
така числото X,
зададено в
примера, се
представя по
следния
начин:
В
примера е
използвано
число, чиято
мантиса
съвпада с
коренуваното
в пример №189
число, така
че
използвайки
този
резултат,
записваме:
Окончателно
се получава
следния
резултат:
Като
се има
предвид
изложеното
току що,
съвсем разбираемо
е защо в
алгоритмичните
езици се изисква
функцията
корен втори
да получава аргумент
от реален
тип.
За
добро
усвояване на
темата,
препоръчваме
на читателя
да се потруди
върху
следващите
въпроси и
задачи:
1. Като
използува
примерите,
представени
в разделите
IV,V,VI,VII, читателят
следва да
задълбочи
разбирането
и умението си
върху даден
алгоритъм,
върху
логическата
структура и
микропрограма
за
функциониране
на съответното
устройство.
За целта той
може да избира
произволни
стойности на
съответните
операнди,
като не
забравя, че
не всяка стойност
ще доведе до
преминаване
през най-интересните
клонове на
алгоритмите.
Отделен
интерес
представляват
стойностите
на аргументите,
при които се
получава за
резултат
минималното,
максималното
число,
числото нула или
съответният
признак на
резултата.
Специално
изучете
признаците
на резултата
формиращи се
в
устройството
за работа с
плаваща
запетая.
2. Проверете
верността на
логическите
функции за
откриване на
препълването,
когато
числата са
представени
в бройна система
различна от
двоичната.
3. Установете
влиянието на
модифицираните
кодове върху
алгоритмите.
4. Обяснете
защо не е
желателно
изменението на
фомàта
, в който се
представя
резултатът
от дадена
операция. До
какви
проблеми би
довело
изменението
му, при изпълнение
на
последователни
операции, в
които като
операнд се
използува
всеки резултат
от предидуща
операция.
Какви според
Вас са
проблемите
на такова
динамично
изменение на фомàта.
5. Разгледайте
известна Ви
система от
машинни
команди и
съпоставете
множеството
изпълними
операции,
които тя
реализира, с
разгледаните
в тази книга.
6. Дайте
конкретни
примери, в
които е
необходимо
да се
различава
видът на
препълването.
Посочете
актуалните
(изпълнените
с реален
смисъл) признаци
на резултата
от всяка
операция.
7. Обърнете
особено
внимание на
точността на
изчисленията,
на степента
на
абсолютната
и
относителната
грешки.
Изследвайте
верността на
основните
математически
закони и се
убедете във
верността
или
неверността
на тъждествата,
представени
в [1].
Изследвайте
различните
схеми за
закръгляне и
тяхната
инициализация
в устройството
за работа с
плаваща
запетая.
8. Изграждайте
система от
изводи, които
ще ви помогнат
да
програмирате
по-прецизно,
да постигате
програми,
създаващи
минимум
проблеми.
Следващият
раздел е:
Заключителни
бележки на
автора