ГЛАВА 5
Средства за
асинхронно
управление
Resources for asynchronous control
|
5.3. Краен автомат
с променлива
продължителност
на
микротакта |
|
5.4. Микропрограмен
автомат с
променлива
продължителност
на микротакта
|
В тази глава са представени изследвания, посветени на класическите структури за логическо управление. Класическите подходи за логическо управление чрез обособени (в смисъла на декомпозиционния модел на В. М. Глушков) управляващи крайни автомати не могат да бъдат отречени, защото те имат своите безспорни достойнства. Те ще продължават да бъдат прилагани, което обаче не пречи да бъдат усъвършенствани.
Асинхронната
идея за
управление
определя
съдържанието
на тази
глава. В
началото е представена
една
достатъчно
пълна колекция
от средства
за
генериране
на управляващи
импулси,
които са
функция на
събития в логическите
сигнали. Те
представляват
основното
средство за
реализация
на асинхронния
метод за
управление. В
духа на
асинхронното
управление
по-нататък са
изследвани
структури на
крайни
автомати,
определени
като апериодични.
Това са
тактувани
автомати,
които обаче
реализират
променлива
продължителност
на отделните
микротактове.
Изследвани
са структури
на
апериодичен
краен
автомат с апаратно
закрепена
логика и на
апериодичен автомат
с програмно
закрепена
логика. Представените
структури са
общи,
независещи от
алгоритъма
за
управление,
ето защо могат
да се
разглеждат
като методи
за синтез на апериодични
автомати.
5.1.
Генериране
на сигнали за
асинхронно
управление
Представени
са
логическите
схеми за генериране
на
необходимите
при
асинхронно
управление
събитийни
сигнали и са
пояснени техните
параметри и
възможностите
за манипулиране
на
стойностите
им.
Представени
са условните
им графични означения,
използвани в
структурните
схеми.
Синтезирана
и изследвана
е оригинална логическа
схема за
асинхронна
селекция на
единичен
синхронен
импулс.
5.1.1.
Детектори
на фронт
Детекторите
на фронт,
фронт-детектори
или още
пулс-генератори
са логически схеми,
които
прихващат
фронта на
превключване
на
правоъгълен
сигнал и
формират синхронен
с него
краткотраен
логически
импулс, т.е.
правоъгълен
импулс. В
този смисъл
тези схеми
могат да се
определят
като реагиращи
на събитие,
т.е.
събитийни.
Основното
предназначение
на
генерираните
от
фронт-детекторите
импулси е да
управляват
разнообразни
по
интерпретация
микрооперации
“запис”, като
например
нулиране,
установяване,
изместване,
отброяване,
зареждане с
начална стойност.
Необходимата
продължителност
на тези импулси
се определя
от
изискванията
на елементите,
за които те
са
предназначени.
Ако в синхронните
схеми
основната
причина за настъпило
събитие е единичен
или нулев
импулс, то в асинхронните
схеми основната причина
за събитията
е появата на
фронт. В този
смисъл
потенциалното
наличие на
една
логическа стойност
не е причина
за събитие, а
в определени
условия
константната
логическа
стойност
може да бъде
причина за
предотвратяване
на желано
събитие. Под
събитие
разбираме превключване.
Като имаме
предвид, че в
асинхронните
логически
схеми се
използват
преди всичко
тригери от
тип Latch,
работещи по
ниво,
потенциалните
сигнали много
често могат
да се окажат
в забранени за
тригерите
комбинации.
Ето защо
тяхното управление
се осъществява
чрез
кратковременни
импулси, освен
ако това не
се налага.
5.1.1.1.
Детектор на
преден фронт
а)
Неинвертиращ
Схемата
на детектора
има един вход
и един изход.
Тя генерира
синхронен с
появилият се по
предния
фронт кратък
единичен
импулс, както
е
илюстрирано
на схемата.

Фиг. 5.1.1. Фронт-детектор
Логическата
схема
съдържа нечетен
брой N
последователно
свързани
инвертори.
Така в
схемата И
постъпва
сигналът In и
неговата
закъсняла
инверсия. В
резултат на
тяхното
логическо
умножение се
получава
единичният
импулс Out, който
има
продължителност
Tout=N.τ, където
с t е
означено
закъснението,
което внася
един инвертор.
Следователно
N е
параметър, с
който може да
се регулира
ширината на
генерирания
импулс. При
това регулиране
се постига
отместване
на задния
фронт на импулса
спрямо
предния.
На
фигура 5.1.1 е
показана
логическата
схема, времедиаграмата
и условното
графично означение
на
фронт-детектора.
Следващата
схема e построена
чрез
подходяща
модификация
на предходната
схема. В нея
са
реализирани
два изхода Out1 и Out2. В
отговор на
постъпващ в
схемата
преден фронт,
тя ще
генерира два
различни по
продължителност
импулса, но
те ще бъдат
синхронни по
преден фронт
с входния.
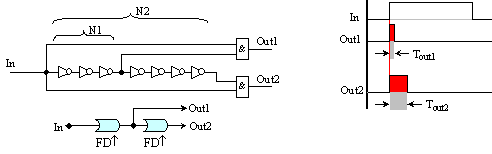
Фиг. 5.1.2. Фронт-детектори
От
схемата се
вижда, че
по-дългата
последователност
N2 генерира
по-широк
импулс, чиято
продължителност
се определя
аналогично.
По
подобен
начин за
целите на
управлението
могат да се
генерират
различни по
количество и
продължителност
импулси.
б) Инвертиращ
Ако в отговор на постъпил преден фронт са необходими инверсни импулси, изходните схеми И могат да бъдат допълнени с инвертор.
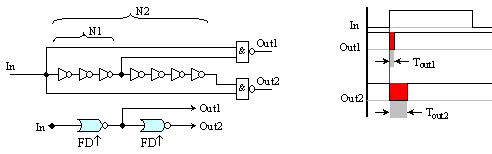
Фиг. 5.1.3. Фронт-детектори
5.1.1.2.
Детектор на
заден фронт
а) Неинвертиращ
Схемата на детектора има един вход и един изход. Тя генерира синхронен със задния фронт кратък единичен импулс, както е илюстрирано на схемата.

Фиг. 5.1.4. Фронт-детектор
Логическата
схема
съдържа нечетен
брой
последователно
свързани инвертори.
Така в
схемата ИЛИ
постъпва
сигналът In и
неговото
закъсняло
отрицание. В
резултат на
тяхното
логическо
събиране се
получава
единичният
импулс Out, който
има
продължителност Tout=N.τ,
където
с t е
означено
закъснението,
което внася
само един
инвертор, а с N
броят на
последователно
свързаните
инвертори.
Следователно
N е
параметър, с
който може да
се регулира
ширината на
генерирания
импулс. Това
се постига
чрез
отместване
на задния
фронт на импулса
спрямо
предния.
Следващата
схема, която
има два изхода
Out1 и Out2, ще
генерира
съответно
два различни
по продължителност
импулса, но
те ще бъдат
синхронни по
преден фронт
с входния.
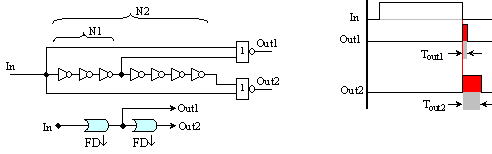
Фиг. 5.1.5. Фронт-детектори
б) Инвертиращ
Ако са
необходими
инверсни
импулси,
изходните
схеми ИЛИ
могат да
бъдат с
неинвертиращ
изход, при
същите
параметри на
предходната
схема.
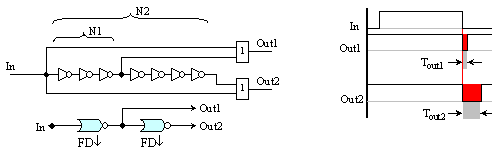
Фиг.
5.1.6. Фронт-детектори
5.1.1.3.
Детектор на
последователни
фронтове
Тази
логическа
схема
маркира и
двата фронта
на единичния
входен импулс,
като
генерира
кратък
единичен импулс
в отговор на
предния и на
задния фронт.
Схемата на
този
детектор е
комбинация
от вече
пояснените.
Продължителността
на изходните
импулси може
да бъде
различна.

Фиг.
5.1.7. Симетрични
фронт-детектори
В
логическата
схема са
използвани
въведените
вече условни
графични
означения.
а) Неинвертиращ
Показаният по-горе фронт-детектор е точно такъв. На следващата фигура обаче е показан алтернативен вариант на неинвертиращ фронт-детектор. Схемата му съдържа два пъти по-малко на брой инверторни елементи. Освен тях схемата съдържа и елемент за логическата функция неравнозначност.

Фиг.
5.1.8. Симетрични
фронт-детектори
Продължителността
на
генерираните
импулси е еднаква
и се определя
от броя на
последователно
включените
елементи в
паралелната
входна
верига.
Когато тези
елементи са
инвертори,
техният брой
следва да
бъде четен,
т.е. Tout=2.K.τ.
б) Инвертиращ
Логическата
схема на
инвертиращ
фронт-детектор
и по двата
фронта
съдържа
верига от
четен брой
последователни
инвертори и
елемент за
логическата
функция
равнозначност.
Продължителността
на изходните
импулси е
еднаква.

Фиг.
5.1.9. Симетрични
фронт-детектори
Във времедиаграмите на представените до тук схеми не е отчитано закъснението на изходния елемент. Това закъснение е само един фронт. То е неизбежно и не е причина да се отхвърля синхронността между входния и изходния сигнал.
5.1.2.
Симетрични
закъснителни
вериги
Процесите на управление на микрооперационно ниво много често се нуждаят от кратко задържане (закъснение) на сигналите във времето. Ако една логическа стойност се появи в точка А, но трябва да достигне точка В по-късно във времето, тъй като там все още няма условия тя да бъде възприета, то тя трябва да бъде задържана. Така в точка В логическата стойност ще се яви със закъснение. Става дума за закъснение, продължителността на което може да бъде настройвана и което няма смисъла на закъснението на фронта от едно превключване.
Симетрична
закъснителна
верига е тази
верига, която
създава на
своя изход
пълно копие
по форма и
параметри на
входния
сигнал, но
след
известно
време, т.е. със
закъснение. С
други думи
входният
сигнал е
изместен във времето
и понеже това
изместване е
едно и също и
за предния и
за задния
фронт на входния
импулс,
веригата се
нарича симетрична.
Така
продължителността
на изходния
сигнал
съвпада с
тази на
входния.
5.1.2.1.
Неинвертиращи
симетрични
закъснителни
вериги
а) По
преден фронт
Казаното по-горе е илюстрирано на следващата фигура. Показана е времедиаграмата и условното графично означение на елемента.
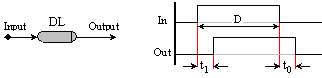
Фиг.
5.1.10. Симетрично
закъснение
Изходният
импулс има
същата
продължителност
D (Duration) еднаква с
тази на
входния. Закъсненията
на
фронтовете
са еднакви: t1=t0.
б)
По
заден фронт
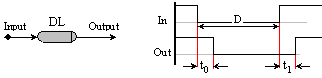
Фиг.
5.1.11. Симетрично
закъснение
Най-често
такива
закъснения
се постигат чрез
последователно
включване на
няколко еднакви
логически
елемента,
които натрупват
последователно
своето
собствено
закъснение.
Когато се
използват
логически
инвертори, за
да бъде
веригата
неинвертираща,
техният брой
трябва да
бъде четен,
както е
показано на
следващата
фигура.

Фиг.
5.1.12. Схема
на
симетрично закъснение
5.1.2.2.
Инвертиращи симетрични
закъснителни
вериги
Ако закъснелият сигнал трябва да се появява с инверсната си стойност, броят на инверторите следва да бъде нечетен. По този начин закъснението, например, по заден фронт ще изглежда така
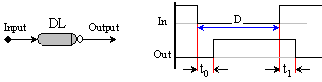
Фиг.
5.1.13. Означение
на
закъснение с
инверсия
5.1.3.
Асиметрични
закъснителни
вериги
Асиметрична
закъснителна
верига ще
бъде всяка
верига, която
създава на
изхода си сигнал,
който не е
копие на
входния. С
други думи
параметрите
на сигнала са
различни, т.е.
различни са закъсненията
на
фронтовете t0¹t1, а от там
и
продължителностите
на съответното
(високо или
ниско) ниво
на входния, в
сравнение с
изходния
сигнал.
5.1.3.1.
Закъснение
само на
преден фронт
За
отместване
във времето
на предния
фронт на
единичен
импулс се
предлага
следната
логическа
схема
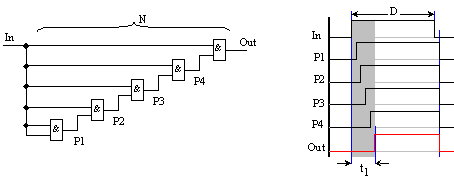
Фиг.
5.1.14. Закъснение
на преден
фронт
Ако
се
пренебрегне
закъснението
на изходната
схема И, може
да се приеме,
че изходният
сигнал е
скъсен по
преден фронт
с N
последователни
закъснения,
внесени от последователно
свързаните N
елемента И.
Така за
крайното
закъснение
можем да
дадем
следната
количествена
оценка t1=N.τ,
където с t е
означено
закъснението
на един
елемент И.
Забележка: при
този вид манипулация
на сигнала
следва да се
разбира, че
отместването
на предния
фронт на изходния
сигнал е за
сметка на
неговата
продължителност,
т.е. при
отместване
по-голямо от
продължителността
D, на изход ще
се получава
константа “0”.
За представяне на този вид закъснителни вериги ще използваме следното условно графично означение
![]()
Фиг.
5.1.15. Означение
на
закъснение
на преден
фронт
Този тип закъснение може да се постигне и със симетрична закъснителна верига, като за целта се изгради следната схема
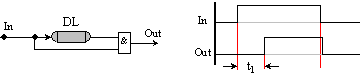
Фиг.
5.1.16. Асиметрично
закъснение
на преден
фронт
Ефектът
от
симетричното
закъснение
се премахва
от
логическото
умножение на
закъснелия
импулс с
входния.
Задният
фронт на импулса
Out е
синхронен с
този на входния,
с отчитане на
закъснението,
внасяно от
схемата И.
5.1.3.2.
Закъснение
само на заден
фронт
За отместване във времето на задния фронт на единичен импулс се предлага следната логическа схема
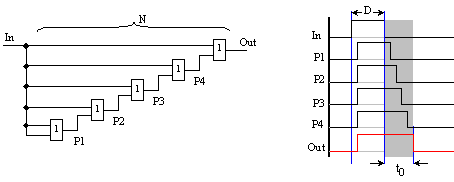
Фиг.
5.1.17.
Асиметрично
закъснение
на заден
фронт
Ако се пренебрегне закъснението на изходната схема ИЛИ, може да се приеме, че изходният сигнал е удължен по заден фронт спрямо входния импулс. Можем да твърдим, че изходният импулс е синхронен по преден фронт с входния импулс.
Задният
фронт на
изходния
импулс е
отместен във
времето на N
последователни
закъснения,
внесени от последователно
свързаните
елементи.
Така за
крайното
закъснение
можем да
дадем следната
количествена
оценка t0=N.τ, където
с t е
означено
закъснението
на един
елемент.
Забележка: при
този вид
манипулация
на сигнала не
съществува
опасността,
за която
предупредихме
в предходния
случай. С
други думи удължаването
на сигнала
чрез
отместване на
задния му
фронт е
неограничено.
За означаване на този вид закъснителни вериги ще използваме следното условно графично означение
![]()
Фиг.
5.1.18. Означение
на
закъснение
на заден
фронт
5.1.4.
Комбинация
от
симетрични и
асиметрични
вериги
Чрез комбинацията на симетрични и асиметрични закъснителни вериги може да бъде постигнато всякакво взаимно разположение на два и повече импулса, които са дъщерни на един единствен входен импулс. Например, често за надеждно изпълнение на микрооперация запис, регистрите се комплектуват с два сигнала – “разрешение” и “запис”. Надеждността на записа се осигурява когато записващият импулс е вложен във времето спрямо разрешаващия импулс. Следващата логическа схема може да осигури описаната ситуация.
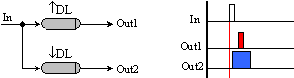
Фиг.
5.1.19. Комбинация
от
закъснителни
схеми
Ако продължителността на входния импулс е недостатъчна за осъществяване на превключването на логическия възел, към който е подаден манипулираният импулс, то продължителността на последния може да бъде допълнително увеличена. Това може да бъде постигнато със следната логическа схема.
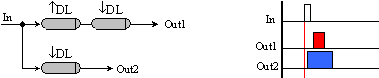
Фиг.
5.1.20. Комбинация
от
закъснителни
схеми
След
първоначалното
задържане на
входния
импулс In чрез
симетричната
закъснителна
верига, той е
допълнително
разширен с
помощта на асиметричната
закъснителна
верига по
заден фронт.
Така, в резултат
на
комбинацията
от двете
вериги, импулсът
Out1 е
допълнително
разширен.
Продължителността
на изходния
импулс Out2 е също
допълнително
увеличена.
5.1.5. Сигнал
за край на
превключване
на тригер
В
случай,
когато едно
микроконвейерно
звено не извършва
манипулация
на данните,
т.е. когато неговата
операционна
логика
липсва, тогава
като
микрооперация
остава само
записът на
данни в
неговия
регистър
фиксатор.
Тази микрооперация
запис е много
кратка. Нейното
закъснение е
равно на
времето за
превключване
на тригерите,
което
обикновено е
от 2.t до 6.t. Събитието
“край на
превключването”
е необходимо
да се
маркира, тъй
като то
представлява
сигнал, който
управлява
конвейерния
автомат. На
фигура 5.1.21 е
показана принципна
логическа
схема, която
е способна да
реши така
описаната
задача.
Въпреки, че
схемата е
приложена за
елементарен
RS-Latch тригер, тя
може да се
приложи и
върху други по
тип тригери.
Схемата
работи по
един и същи
начин и за
двете
превключвания
0®1 и обратно 1®0.
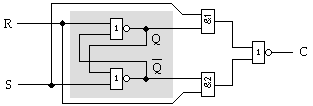
Фиг.
5.1.21. Логическа
схема на
тригер със
сигнал за край
на записа
Функционирането
на схемата ще
поясним чрез
времедиаграмата
от фигура 5.1.22.
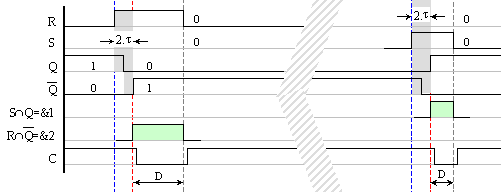
Фиг.
5.1.22. Времедиаграма
за край на превключването
Началното
състояние на
тригера е Q=1. С
подаване на
единица на R
входа
тригерът се
нулира Q=0, но за
достигане на
стабилно
състояние са необходими
минимум (2.t) секунди.
Това е
собственото
му време на
превключване
от едно
състояние в
друго.
Въпреки, че
единицата на
входа R
продължава
да е активна,
други
превключвания
няма.
На
изхода С,
който ни
интересува
се вижда, че
схемата
генерира в
отговор на
превключването
отрицателен
импулс. Този
импулс има активна
стойност
нула през
цялото време
D след
превключването
и до края на
активната стойност R,
породила
превключването.
Именно тази
нула може да
се възприема
като признак,
че имало
превключване.
Нейното
начало
маркира края
на
фактическото
превключване
на тригера.
Аналогичен е
процесът при
обратното
превключване,
което
причинява
единицата
постъпила по
входа S.
Предният
фронт на сигнала
С маркира
момента, в
който се
появява неактивната
комбинация R=0 и S=0.
5.1.6.
Асинхронна
селекция на
импулс
Въпросът за синхронността в действията, протичащи в една схема, е особено актуален. Тук ще бъде разгледана задачата за селекция (отделяне, изрязване) на единичен логически импулс от някаква последователност, било тя с постоянна честота или не. По същество следва да разбираме, че има събитие, в отговор на което от явяващите се в дадена точка импулси, трябва да бъде отделен първият цял. В този смисъл отделеният ще бъде копие във времето на своя първообраз, т.е. ще бъде напълно синхронен с него и по преден и по заден фронт. Това трябва да става в отговор на друг импулс, нямащ нищо общо с последователността от импулси, т.е. той е напълно асинхронен по отношение на нея.
Като
решение на
така
поставената
задача тук е
предложена
логическата
схема от фигура
5.1.23. Тя е
синтезирана
с
разбирането,
че нейното
превключване
ще започне след
изчезване
на външния
асинхронен
импулс Р. На
вход С ще
постъпват
импулси от
последователността,
които
подлагаме на
селекция.
Схемата работи
без да зависи
от
продължителността
на входния
сигнал Р, а
след
селекцията
се установява
в изходно състояние.
За да бъде
облекчено
илюстрирането
на процеса
селекция в
схемата и във
времедиаграмата,
последователността
от импулси С
е представена
като
периодична.
Схемата
съдържа два
тригера –
първият е от
тип Т,
асинхронен, с
динамично
управление,
превключващ
се по заден
фронт
(структура Edge),
вторият е от
тип RS,
асинхронен,
превключващ се
по ниво
(структура Latch). Тя
използва и
двете фази на
последователността
С. Обратната
връзка от
изхода към
входа е
въведена за
възстановяване
на схемата в
изходно състояние.
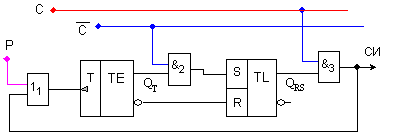
Фиг. 5.1.23. Логическа
схема на
селектора
В
нормално
(изходно)
състояние,
когато отсъства
входен
сигнал Р,
двата
тригера са
нулирани (QT=QRS=0) и
логическите
схеми И2 и И3 са
“затворени”.
Когато се
появи входен
импулс Р, той
преминава
през схемата
ИЛИ1 и попада на
входа на
Т-тригера.
Последният
се превключва
при
изчезването
му, т.е. по
задния фронт.
Появилата се
единица на
изхода QT
отваря
схемата И2.
Независимо в
кой момент се
е отворила
тя, първият
единичен
импулс (или
част от него)
излязъл на
нейния изход,
преобръща с
нарастващия
си фронт
следващия RS-тригер
в състояние
единица (QRS=1). Той
от своя
страна
отваря
следващата
схема И3, през
която трябва
да премине
импулс от
последователността
С. Характерно
е, че това става
предварително,
в момент,
когато С=0.
Появилият се
в
последствие
импулс в
последователността
С преминава
през
отворената
вече схема И3
на изход в
качеството
си на селектиран
(отделèн)
импулс (СИ). В
същото време,
по обратната
връзка, този
импулс
постъпва на
входа на
Т-тригера,
който се
преобръща по
задния му
фронт отново
в нулево
състояние.
Така той
затваря
схемата И2 и
едновременно
с инверсния
си изход
нулира
RS-тригерът, който
пък запушва
схемата И3.
Описаните
превключвания
са
лавинообразни
и когато завършат,
схемата се
оказва
отново в
стабилното
изходно
състояние, в
което очаква
нова поява на
асинхронен
импулс по
входа Р, като
при това е
нечувствителна
на импулсите
от последователностите
С и notC.
Описаните
превключвания
са
изобразени в два
варианта на времедиаграмата
от фигура 5.1.24.
Първият вариант
представя
импулсът Р с
продължителност
по-голяма от
един период,
а във втория
вариант
продължителността
му е по-малка
от периода.
Периодичността
на
изобразения
сигнал е
условна (само
за удобство).
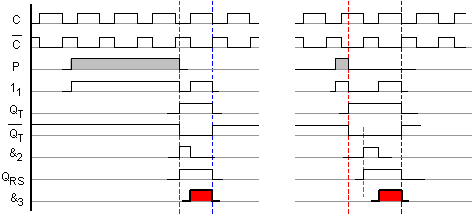
Фиг. 5.1.24. Времедиаграма
на
селектиране
На фигура 5.1.25 е показана принципната логическа схема на селектора, който използва само една от фазите на входната импулсна последователност.
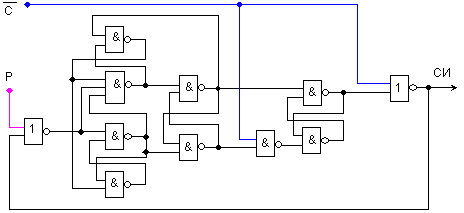
Фиг.
5.1.25. Принципна
логическа
схема на
селектора
Получената
логическа
схема може да
бъде оптимизирана,
ако се
отслаби
изискването
относно
продължителността
на входния
стартиращ
импулс Р така,
че входният
тригер да
бъде с
по-проста
структура,
вместо тази
от тип Edge.
За да е
възможно
това,
продължителността
tp на
импулса Р
следва да
удовлетворява
неравенството
![]()
където с
буква Т е
означен
периодът на
последователността
С, а с τc продължителността
на единичния
импулс в същата
последователността
С. Тези
оценки са
индивидуални,
когато
последователността
не е с
постоянна
честота.
Окончателната логическа схема, чийто синтез е съобразен с идеята за оптимизиране, изказана по-горе, е представена на фигура 5.1.26.
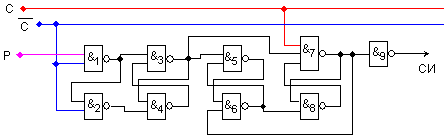
Фиг. 5.1.26. Оптимизиран
вариант на
логическата
схема на
селектора
Неравенството
(5.1.1) осигурява
на
конюнкцията (PÇnotC)
възможността
да пропусне
поне един цял
импулс от
последователността
notC при
произволна
асинхронност
на импулса Р. Поради
това, че
схемата
загуби елемента
с динамично
управление,
тя сработва
по ниво и
селектира
първия
единичен импулс
от
последователността
С, който се
вписва
изцяло в
импулса Р
след неговия
преден фронт.
Оптимизирането
се изразява в
намаления
брой
логически
елементи. По
сравнение с
някои
известни от
литературата
решения,
състоящи се
от два
последователни
D-тригера
с динамично
управление,
както и в сравнение
със схемата
от фигура 5.1.25,
съкращението
на
логическите
елементи в
предложената
логическа
схема е на
цели 25% !
На
фигура 5.1.27 е
представена
времедиаграмата
за селектиране
на единичен
импулс от
оптимизираната
схема на
селектора. В
нея са
изобразени три
опита за
селекция,
единият от
които не е успешен.
Подаваните
асинхронни
импулси Р са с
различна
продължителност,
която, когато
не
удовлетворява
въведеното
ограничение
чрез по-горе
записаното
неравенство,
води до
неуспех, т.е.
на изхода на
схемата не се
явява
логически
импулс. Такъв
е вторият от
случаите,
показани на
времедиаграмата. Селектираният
импулс СИ е
вписан по
време в
асинхронния
импулс Р.
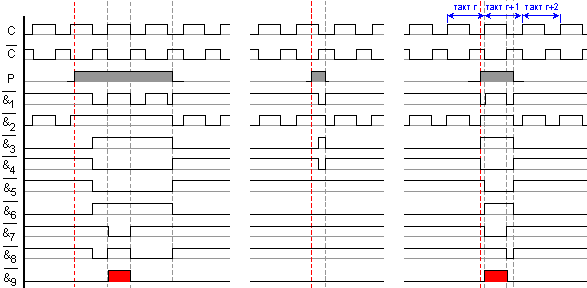
Фиг. 5.1.27. Времедиаграма
на
селектиране
Искаме
да разкрием
още една
възможност
на логическата
схема от
фигура 5.1.23,
която се изразява
във
възможността
да не бъде
осъществена
обратната
връзка от
изхода на елемент
И3 към вход на
елемент ИЛИ1.
При липса на
тази връзка
няма да се
разпространи
възстановяващ
схемата
импулс, като
по този начин
елементът И3
ще остане
“отворен” и на
неговия
изход ще
продължават
да излизат до
безкрайност
импулсите от
последователността
С. Излизането
на импулси ще
бъде прекратявано
при втори
входен
сигнал Р. В този
смисъл,
такава
модификация
на схемата
може да се
разглежда
като
генератор на
тактови
импулси,
синхронни с
изначалната
тактова
последователност,
генерирани в старт-стопен
режим. Тази
възможност
може да бъде
реализирана във
всяка от
модификациите
на селектора.
5.2.
Синхронизация
на
асинхронни
сигнали със синхронни
Въведение
Поставената
тук тема се
разглежда в
условията на
конвейерно
звено, което
реализира изчислителен
процес под
управлението
на собствен
тактов генератор.
Така се
разбира, че
имаме
предвид сложно
и
многотактово
звено.
Структурната
ситуация,
която ще
поясним, е
илюстрирана
на фигура 5.2.1.
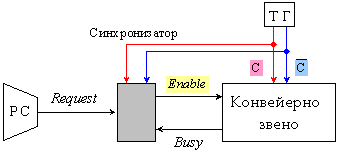
Фиг. 5.2.1. Роля и
място на
синхронизатора
Както
изяснихме в
глава 3,
такива
конвейерни
звена, с цел
висока
надеждност,
се обслужват
от повече
сигнали от
тип SS (status signals) и CS (control signals).
Техният
минимален
състав беше
въведен и най-подробно
изяснен в
раздел 3.2.
Всичко казано
там беше
насочено
преди всичко
към синтеза
на конвейерния
автомат,
способен да
управлява такива
звена.
Правилното
стартиране и
функциониране
на
конвейерното
звено изискваше
наличие в
състава му на
структурен
елемент,
наречен синхронизатор.
Задачата на
този елемент
беше да
синхронизира
появата на
асинхронния
сигнал Request, с
който
конвейерният
автомат PC иска
да стартира
звеното,
което
управлява, с
импулсите в
тактовата
последователност,
под
упралението
на която
работи то.
Този сигнал
не е способен
веднага да
стартира
изчисленията
в звеното, а
само иска това
да стане, ето
защо и се
нарича
“заявка”. Самото
стартиране
на
изчислителния
процес в
структурата
на
конвейерното
звено зависи
от неговото
състояние,
както и от
тактовата
последователност,
която
развива алгоритъма.
За
стартиране
на
изчислителния
процес в такива
конвейерни
звена е
необходим
разрешаващ
импулс Enable.
Разрешението
трябва да
допусне
тактовата
последователност
до
структурните
елементи на
звеното. В
този смисъл
разрешението
трябва да се
появи синхронно
по отношение
на тактовата
последователност.
Колко време
то ще бъде
активно и в
кой момент ще
изчезне, това
зависи от
функцията и
от
конструкцията
на
конвейерното
звено. Тези
два
параметъра
на сигнала Enable не са
проблем в
неговия
синтез. Тук
ще приемем,
че
продължителността
на този
импулс следва
да бъде не
по-малка от
периода на
тактовата
последователност.
С такава
продължителност
може да се
осигури поне
един цял синхронен
импулс, който
да се
използва за
непосредствено
стартиране
на
изчислението.
Представата
за
развитието
на процеса на
синхронизиране
ще
илюстрираме
чрез
времедиаграмата
от
следващата
фигура.
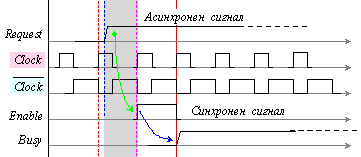
Фиг. 5.2.2. Времедиаграма
на процеса
синхронизация
От
горните две
абсциси се
вижда, че
сигналът Request,
който идва от
конвейерния
автомат РС
(вижте фигура
5.2.1), се появява
асинхронно, в
случая по
средата на импулс
от
последователността
Clock. Предният
фронт на
заявката
може да се
появява
случайно в
рамките на
произволен
текущ период
на тактовата
последователност.
Тази случайност
формира една
латентност
(по ширината
на сивата
ивица), която
е неизбежна,
но нейната
продължителност
не може да
бъде повече
от един
период, ако
синтезът
успее да
осигури
появата на сигнала
Enable
по първия цял
импулс от
тактовата
последователност.
Зелената
стрелка във
времедиаграмата
сочи момента,
в който се
появява
сигналът за разрешение.
Минималната
продължителност
на това
закъснение
се цели по
разбираеми причини
– стартиране
на
изчисленията
без никакво
забавяне!
Следващия
период
конвейерното
звено следва
да бъде под
въздействието
на тактовите
импулси –
започва
изчислението
в операционната
структура. С
това, след не
повече от
един период,
следва да
възникне и
сигналът Busy, определящ
състоянието
на
конвейерното
звено като
“заето”.
Ще
приемем, че сигналът
Enable
следва да
изчезна след
изтичане на
един период
от тактовата
последователност,
което е
изобразено
на
времедиаграмата.
Това положение
не е
задължително,
всичко
зависи от
това, дали
по-голямата
продължителност
на сигнала
няма да пречи
на нормалната
работа на
звеното.
Логическата
схема, която
ще формира
този импулс
все някога трябва
да се
възстанови,
за да може да
повтори
своята
функция, в
отговор на
следващата заявка
Request.
Логическа схема на синхронизатора
Пояснихме,
че в отговор
на случайно
появяващ се
фронт (може
преден, може
заден) на
сигнал от тип
Request,
трябва да се
появи сигнал,
чиито
фронтове да
са в синхрон
с фронтовете
в тактовата
последователност.
Именно
постигането
на това
разбиране се
нарича синхронизация
или още привързване,
както може да
се срещне в
някои
литературни източници.
Логическият
синтез в
подобни случаи,
когато
следва да се
отчита
времето, което
е дискретно,
не се
подчинява на
традиционните
методи за
синтез. Тук
единствено интуицията
и опита на
Конструктора
може да дадат
резултат.
Подобни
ситуации
бяха обобщени
още в
началото на
тази книга, в
първия раздел
на първа
глава, а това
тук е
поредния
пример за
изложените
там
обобщения.
Нашето
разбиране за
процеса,
представен на
фигура 5.2.2,
естествено
ни навежда
към необходимостта
за запомняне
на събитието
“поява на
заявка”, т.е. за
използване
на тригер.
Ето защо ще
разгледаме
следните
логически
схеми
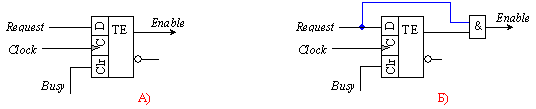
Фиг. 5.2.3. Синхронизатор
И в
двете схеми е
използван е
динамичен D-тригер
със
структура Edge,
което е
основен
подход при
синхронизиране
на
асинхронни
сигнали.
Фиксирането
в тригера на
логическата
стойност на
сигнала Request
става в
момента на
предния
фронт на
тактов импулс,
който
постъпва на
вход С.
Импулсите от
серията Clock
причиняват
многократни
фиксации на
логическата
стойност по
входа D.
При това
положение,
липсата на
заявка води до
състояние
нула на
правия изход
на тригера.
Ако моментът
на поява на
импулса Request е
пропуснат,
както е
изобразено
на времедиаграмата,
фиксацията
се постига
при предния
фронт на
следващия
тактов
импулс. За да
се гарантира
надеждното
фиксиране обаче,
върху
входната
асинхронна
стойност следва
да се наложи
ограничение.
Тази стойност
трябва да се
поддържа във
времето в продължение
на следното
време:
![]()
където
с tReq е
означена
продължителността
на сигнала Request;
с Т
е
означен
периодът на
сигнала Clock;
с τ1 е означена
продължителността
на единичния
импулс в
сигнала Clock.
Ако
сигналът Request има
много
по-голяма
продължителност,
за да се
осигури
исканата
продължителност
за сигнала Enable, се
използва
принудително
изчистване
на тригера,
по входа Clr (Clear).
Следва
да се
отбележи, че
този вход е
приоритетен
и ако към
него е
подключен
сигналът Busy,
който е
активен в
продължение
на целия изчислителен
цикъл, то
това
продължително
и приоритетно
удържане на
тригера в
нулево състояние
е гаранция за
висока
надеждност и
изключване
на
възможността
за запис в тригера,
което би
довело до
лъжливи
стойности за
сигнала Enable на
неговия
изход. В
частта Б) от
фигура 5.2.3, е
предложена
допълнителна
застраховка
към
разрешаващия
сигнал, който
е невъзможен
ако липсва
заявка. И
двете схемни
решения
осигуряват
процеса,
представен
на фигура 5.2.2.
Производни схеми
Разглеждаме
функционирането
на долната схема
при входния
сигнал R.
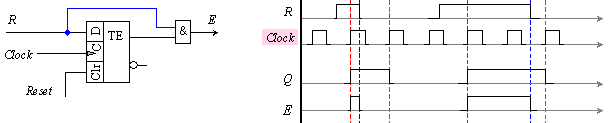
Фиг. 5.2.4. Синхронизатор само
на преден
фронт
Показаната
схема
синхронизира
асинхронния
сигнал R само
по преден
фронт на Clock. От
времедиаграмата
може да се
види, че
правият
изход
на тригера
генерира сигнал,
на който и
двата фронта
са синхронни
по предния
фронт на Clock.
Следващата
схема
синхронизира
сигнала R и по
двата фронта
на импулсите
в тактовата
последователност
Clock.
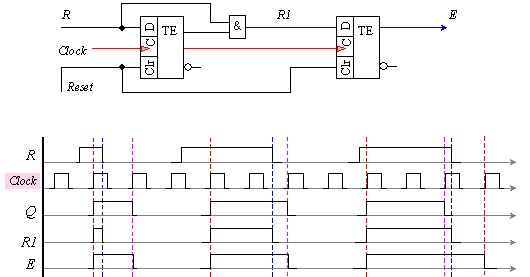
Фиг. 5.2.5.
Синхронизатор
на преден и
на заден фронт
Добре
е да се
обърне
внимание на
факта, че правият
изход Q на
левия тригер,
е също
синхронен
сигнал, но за
разлика от
него,
изходът E има
заден фронт винаги
след
изчезване на
асинхронния
сигнал R.
Разположението
на всеки един
фронт от генерираните
сигнали
следва добре
да се изучи в
множество
различни
ситуации, за
да може
използването
му да бъде с
максимален
ефект.
5.3.
Краен
автомат с
променлива
продължителност
на
микротакта
В този раздел е представен синтезът и изследването на оригинална логическа структура на синхронен краен автомат с апаратно закрепена логика, генериращ променлива продължителност на микротакта. Такива автомати реализират във висока степен асинхронно изпълнение на управляващия алгоритъм и се определят като апериодични. Логическата структура на автомата е обща и не е зависима от конкретен алгоритъм. Това важи за крайни автомати както със структура на Мур, така и на Мили. Изявена е възможността за изпълнение на кратки нано и пикопрограми в рамките на общия управляващ алгоритъм, представляващи последователно развитие на отделно взет микротакт. Структурата осигурява апериодичност включително и на тези нива. Синтезирана е необходимата за реализация на тези възможности допълнителна логическа структура.
Детайлно
описание и
стройна
класификация
на
логическите
структури на
синхронни
крайни
автомати с
апаратно
закрепена
логика
читателят
може да
намери в
учебната
литература.
Възможните
логически
структури на
краен
(управляващ)
автомат с
апаратно
закрепена
логика
(УААЗЛ) са
добре пояснени
в литературата.
Методиките
за
проектиране
на синхронни
управляващи
автомати с
апаратно
закрепена
логика са
също
известни.
Методики за
проектиране
на
асинхронни
УААЗЛ обаче
липсват.
Пример за
синтез на
конкретен и
изцяло
асинхронен
УААЗЛ
читателят
може да разгледа
в книга [3].
В
този раздел
ще
разгледаме
задачата за
проектиране
на УААЗЛ в
условията на
комбинация
от двата
основни
метода за
управление – синхронен
и асинхронен.
Целта е
постигане на
максимално
възможното
бързодействие
при
изпълнение
на
управляващия
алгоритъм в
съчетание с
простотата
на техническата
реализация
при
синхронно
тактуване.
Такива
автомати
могат да
бъдат определени
като
автомати с
променлива
продължителност
на
микротакта
или като
апериодични
автомати и
техни
принципни
схеми в проучените
литературни
източници
също не са
срещнати.
5.3.2. Синтез
на
логическата
структура на
автомата
За
разлика от
микропрограмните
автомати (раздел
5.4), които имат
възможност
да представят
в
структурата
на
микрокомандата
си продължителността
на
мокротакта,
УААЗЛ нямат
тази
възможност.
Това се дължи
на факта, че
тези
автомати не
притежават
памет за
всички
възможни
микрокоманди,
а само за текущата.
Последното
означава, че
продължителността
на текущия
микротакт е
функция на
текущото
състояние на
автомата и
като число не
може да се
съдържа в
структурата
на микрокомандата (разбирай кодовата
комбинация на
текущото
състояние).
От тук
следва, че продължителността
на всеки
микротакт
трябва да се
изчислява,
т.е. да се
възстановява
от кодовата
комбинация
на
състоянието
за всеки
микротакт
отделно.
За
измерване на
продължителността
се използва
брояч.
Продължителността
на всеки микротакт
се оценява
(измерва)
числено от Конструктора,
още по време
на синтеза на
управляващия
алгоритъм, в
брой тактове
на тактуващата
последователност.
За целта се
съставя
кодова
таблица от вида
на
представената
по-долу,
която трябва
да се
използва за
синтез на
шифриращата
комбинационна
схема.
Таблица
5.3.1. Общ
вид на
кодовата
таблица
|
Състояние S(t) |
Продължителност T(t+1) |
|
S0 |
1 период (001) |
|
S1 |
3 периода (011) |
|
S2 |
4 периода (100) |
|
S3 |
2 периода (010) |
|
... ... |
... ... |
Автоматът
се
превключва в
следващото
състояние
само след
изтичане на
времето на текущото
състояние,
което по
принцип
съответства
на следния
граф на
преходите
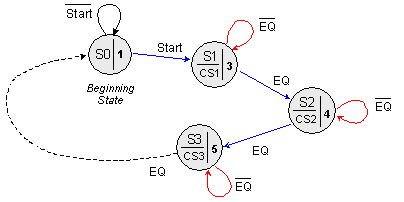
Фиг.
5.3.1. Граф
на преходите
От
графа се
вижда, че при
липса на
сигнал “Start”,
автоматът се
удържа в
изходно
състояние в
продължение
на
неопределен
брой тактове.
Превключването
започва след
появата на този
сигнал, като
продължава
от състояние
към
състояние
само при
условие, че
времето на текущото
е изтекло (EQ=1), плюс,
разбира се,
допълнителните
условия за
преход, имащи
смисъл и
отнасящи се
до конкретния
алгоритъм за
управление.
От тук лесно
може да бъде
съобразено,
че сигналът
за запис на
кодовата
комбинация
на
състоянието
в регистъра
на
състоянието
е функция от
съдържанието
на брояча,
отмерващ
времето.
Заедно с изчисляване
на кодовата
комбинация
на новото състояние S(t+1),
комбинационната
схема на
функциите за
преход в
автомата
трябва да
изчисли (да
шифрира) и
продължителността
на следващия
микротакт T(t+1)
като функция
от
състоянието
T(t+1)=f(S(t)), според
таблица 5.3.1.
Тази продължителност
следва да се
записва в нулирания
брояч като
начално
съдържание.
Този запис
следва да се
извършва
едновременно
със записа на
кодовата
комбинация
на новото
състояние в
паметта на
автомата.
Така на
брояча може да
се гледа като
естествено
допълнение
към регистъра
на кода на
състоянието.
Във
връзка с
направените
съждения е
синтезирана
допълнителната
апаратура към
структурата
на УААЗЛ, за
да може той
да работи с
променлива
продължителност
на микротакта.
Както се
вижда на
фигура 5.3.2, в
долната й
част е
изобразена
логическата
структура на
УААЗЛ, която
съответства
на структурата
на автомат на
Мур.
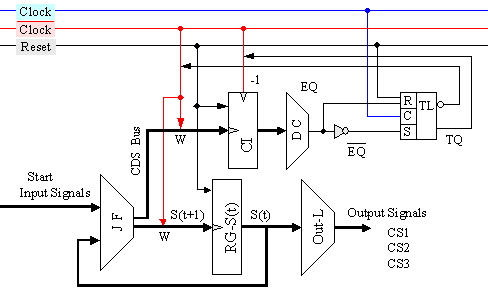
Фиг.
5.3.2. Логическа
структура на
автомата
В
центъра й се
вижда
регистъра на
кода на състоянието
RG-S,
а към
неговите
изходи е
включена
комбинационната
схема Out_L,
реализираща
функциите на изходните
сигнали. Към
входовете на
RG-S
е подведена
новата
кодова
комбинация
на състоянието
S(t+1), изчислена в
текущия
микротакт от
JF – комбинационната
схема,
реализираща
функциите на
преходите (Jump
Functions).
Представената
структура е
проектирана
като
синхронна и
се тактува от
сигнала Clock.
Основната
задача на
допълнителната
апаратура е да
не допуска
всеки тактов
импулс до
входовете за
запис на
регистъра и
на брояча и
да селектира
такива
импулси W
само в
нужните
моменти. Показаното
допълнение
се състои от
декрементен
брояч на
тактови
импулси CI (Counter
Instructions), към
изходите на
който е
включен
дешифратора
DC на
съдържание
нула EQ (EQ=1, ако (CI)=0).
Правата и инверсната
фази на
сигнала EQ от
дешифратора
управляват
състоянието
на
синхронния
RS Latch-тригер.
Този тригер
предпазва
схемата от състезания
в обратните
връзки на
вътрешносхемното
управление
като по този
начин осигурява
пълноценна
форма на
импулсите за
запис W. Чрез
своите
изходи TQ и not(TQ)
той
управлява в
кой момент
импулсите от
инверсната
фаза на
тактовата
последователност
not(Clock) да се
подават в
качеството
им на
декрементни
импулси (-1) към
брояча CI, или в
качеството
им на сигнали
за запис W
към RG-S и към CI.
Функционирането
на
логическата
структура e
илюстрирано
с
времедиаграмата
от фигура 5.3.3.
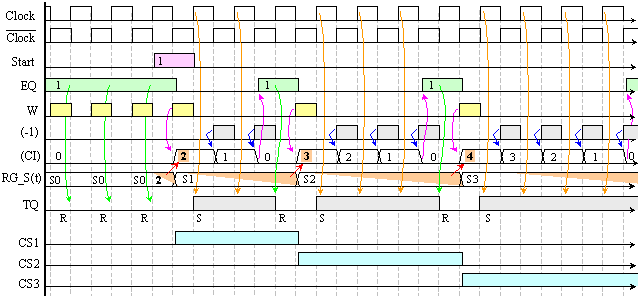
Фиг. 5.3.3. Времедиаграма на
последователността (…S0(1)), S1(3), S2(4), S3(5) …
Микрооперациите
запис в
регистър RG-S и в
брояча CI се
изпълняват
по предния
фронт на импулса
за запис W.
Показана
е
последователност,
съответстваща
на графа на
преходите от
фигура 5.3.1, в
която състояние
S1 се задържа в
продължение
на 3 такта,
състояние S2 – 4
такта,
състояние S3 – 5
такта, а началното
състояние S0, с
продължителност
1 такт, се
повтаря
няколко пъти
в цикъл,
докато не се
появи стартовият
сигнал “Start”. За
правилно
стартиране
на
превключванията
към този
сигнал се
предявяват
определени
изисквания:
·
Сигналът
“Start” да се
появява
синхронно по
предния
фронт на
тактовата
последователност
Clock ;
·
Продължителността
му да е
минимум един
период, както
е показано на
времедиаграмата.
При
това
положение
входната
комбинационна
схема JF
следва да
успее да
изчисли
продължителността
на
състоянието
S1 (за примера това
е числото 2) за
времето
между
предния и задния
фронт на
тактовия
импулс Clock. Във всички
останали
състояния
времето за
аналогичното
изчисление е
многократно
по-голямо,
което следва
да се има
предвид при
синтеза на
шифриращата
схема според
таблица 5.3.1.
На
последните 3
абсциси във
времедиаграмата
са показани
изходни
управляващи
сигнали CS1, CS2 и CS3,
които имат
различна
продължителност,
съответстваща
на тази на
отделните
състояния на
автомата,
приети за
примера.
Логиката на
сигналите
във
времедиаграмата,
реализирани
от
логическите схеми в
структурата
на автомата,
е следната:
Сигнал
за запис W:
![]()
Сигнал (-1):
![]()
Сигнали за
управление
на тригер TL:

Синтезираната логическа структура без изменения може да се приложи и върху крайни автомати със структура на Мили, което я определя като универсална.
5.3.3.
Нанокоманди.
Пикокоманди
Представената
на фигура 5.3.2
структура
предлага
изключително
удобната
възможност за
въвеждане на
нано и
пикокоманди,
при това с
различна
продължителност,
в рамките на
всеки
отделен
микротакт. За
целта е
необходимо
тактовият
генератор да
генерира
различни
синхронни
последователности,
например
като делител
на една първоначална
тактова
последователност.
При това
положение
всички
тактови
последователности
ще бъдат
кратни и
напълно
синхронни с
изходната. В
резултат на
това
продължителностите
на отделните
нанотактове
и
пикотактове
ще бъдат
винаги
кратни на
периода на
съответната
тактова
последователност
и биха могли
да се
реализират
като нано или
като пикопрограми
в рамките на
съответния
микротакт,
при това с
различни
продължителности
на нано и пикотактовете.
Казаното
е
илюстрирано
с
времедиаграмата
от фигура 5.3.4,
където с ncij
са означени
трите
примерни
наноуправляващи
сигнала,
които могат
да реализират
една
възможна
нанопрограма,
съответстваща
на управляващия
сигнал CS1, при
тактуване
чрез сигнал 2.Clock.
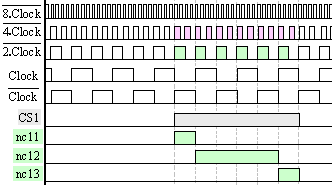
Фиг.
5.3.4. Тритактова
нанопрограма
в рамките на CS1
Друга
възможност е
показана на
фигура 5.3.5 при
използване
на тактовата
последователност
4.Clock. С рсij са означени
примерни
осем
пикокоманди,
които представляват
8 тактово
изпълнение
на пикопрограма,
съответстваща
на същия
управляващ
сигнал CS1.

Фиг.
5.3.5. Осемтактова
пикопрограма
Логическата реализация на показаните на фигура 5.3.4 и фигура 5.3.5 примерни нано и пикокоманди е представена на фигура 5.3.6. Структурата от фигура 5.3.6 следва да се възприема като допълнение към структурата, представената на фигура 5.3.2.
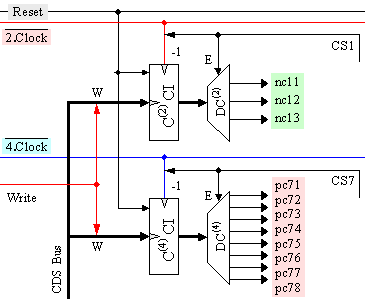
Фиг.
5.3.6. Логическа
структура за
реализация
на нано и
пикоуправляващи
сигнали
Освен
това, следва
да се поясни,
че в тази структура
пикокомандите
се отнасят за
друг управляващ
сигнал,
означен като
CS7. Едновременната
декомпозиция
на един и
същи управляващ сигнал
на две и
повече нива
по принцип е
възможна, но от
техническа
гледна точка
е неразумна. Всеки
основен
управляващ
сигнал CSi, имащ
програмна
реализация
на по-ниско
ниво, работи
със собствен
брояч на
съответната
тактова
последователност,
подобен на
означените
на фигура 5.3.6
броячи C(2)CI или C(4)CI, работещи
с тактовите
последователности 2.Clock и 4.Clock
съответно.
Началното
съдържание на
тези броячи
се зарежда с
помощта на
сигнала W (Write),
чиято логика
е изразена от
уравнение (5.3.1).
Началната
стойност е
същата, като
тази, която
се зарежда в
брояча на
тактови
импулси CI в
основната
структура, но
с отчитане на
коефициента
на кратност.
Така
например, ако
CS1 има
продължителност
от 3 периода
от сигнала Clock,
за да бъде
тази
продължителност
същата в условията
на тактовата
последователност
2.Clock, тя следва
да се удвои в
брояч C(2)CI и да се
учетвори в
брояч C(4)CI. Това се
постига
лесно чрез
лявоизместеното
записване на
началната
стойност в
тези броячи
по сигнал W.
Крайната
реализация
на изходните
нано и пико
управляващи
сигнали ncij,
и pcij, е
постигната
чрез
съответния
дешифратор DC(2) или DC(4) от фигура 5.3.6.
Нанокомандите,
както и
пикокомандите,
които имат
продължителност
по-голяма от
един период,
се
реализират
от дешифраторите
като
дизюнкция от
необходимия
брой
последователни
състояния на
брояча.
Заключение
Синтезираните логически структури представляват оригинално и общо решение на поставения проблем. Те се характеризират с гъвкавост при постигане на конкретни практически решения, не изискват промени в методиката за синтез на крайни автомати с апаратно закрепена логика и във висока степен приближават времевото изпълнение на управляващите алгоритми спрямо съответното им чисто асинхронно изпълнение. В същото време структурите притежават простотата на техническата реализация, характерна за чисто синхронните автомати. Тези характеристики сериозно облекчават практическата настройка на реални системи, в които могат да бъдат приложени.
5.4.
Микропрограмен
автомат с
променлива
продължителност
на
микротакта
Микропрограмните управляващи автомати не противоречат на теорията на крайните автомати. Тяхното достойнство се изразява главно в независимостта на логическата им структура и нейната хардуерна реализация от изменения в управляващия алгоритъм, които се налага да бъдат извършвани, особено често в началните етапи на разработките. Трябва да отбележим, че този подход за разработка се пренася на всички следващи по-високи нива, като например при промишлени управляващи контролери, при управление на обекти и процеси с компютърни системи и комплекси. Софтуерната реализация на управляващите алгоритми в тези системи се постига в пълна степен като независима от хардуерното им осигуряване.
5.4.1.
Променлива
продължителност
на микротакта
Вече
многократно
изтъкнахме,
че стремежът
към
асинхронния
метод за
управление е
твърде силен
поради
неговите
достойнства.
Ето защо
продължаваме
да търсим
възможност
за негова, макар
и частична и
не в
чист вид, реализация
включително
и в този
вариант на
краен
автомат с
програмно
закрепена
логика. Тази
задача е актуална,
и като имаме
предвид
хардуерната
елементна
база,
предоставяща
тази възможност,
тя е
постижима.
Както и в
предходния раздел,
решението ще
търсим чрез
комбиниране
със
синхронния
метод за
управление.
При това
комбиниране
на методите
основен е синхронният
метод, но
външно
управлението
има качествата
на
асинхронния.
Двигател
на
превключванията
в този случай
е тактов
генератор,
който
генерира
непрекъсната
последователност
от тактови
импулси, с
период Т.
Продължителността
на този период
е избрана
така, че да е
достатъчна
за
осъществяване
на най-краткото
превключване
в
логическата
структура на
операционното
устройство.
Като едно от
най-кратките
превключвания,
при това
считано за
типично, може
да бъде
избрано например
превключването
на обикновен
регистър при
изпълнение
на
микрооперация
“нулиране”. Останалите
микрооперации,
свързани с
по-продължителни
превключвания,
като “запис”,
“изместване
съдържанието
на регистър”,
“броене”,
“събиране”,
“мултиплексиране”
и пр., могат да бъдат
оценени по
продължителност
чрез така
избраната
най-кратка.
Оценката на
продължителността
W ще
представлява
цяло
положително
число. Това
число ще
определя
конструкторът,
оценявайки
времето за
превключване
на отделните
логически
възли, като
време за
превключване
в най-тежкия
случай. Формално
тази оценка
може да бъде
изразена както
следва

където с
![]()
е означено
времето за
превключване
на даден
логически
възел при
изпълнение
на j-тата микрооперация,
в най-тежкия
за нея
случай.
Така, при реализация на управляващия алгоритъм, се получава, че отделните микротактове в него ще имат различна продължителност. Тази продължителност на отделните микротактове обаче е определена не от реалните превключвания, а от конструктора съобразно максимално възможното закъснение. Ето защо такава реализация на управлението не постига в пълна степен бързодействието на алгоритъма, гарантирано от идеята на асинхронното управление.
5.4.2.
Структура
на автомата
В блок-схемата на даден алгоритъм оценката за продължителността на микротактовете трябва да бъде посочена явно във всеки изпълним блок, както е показано на фигура 5.4.1, чрез един примерен линеен алгоритмичен участък.
Според примера от фигурата, управляващият сигнал УС13 следва да се подава към даден логически възел, където възбужда i-тата микрооперация, в продължение на 4Т такта. В следващия такт трябва да се подава управляващият сигнал УС72, който възбужда j-тата микрооперация, чиято продължителност е 1Т. Следващият микротакт стартира едновременно две микрооперации: k-тата чрез УС15 и m-тата чрез УС7, но продължителността му се определя от по-дългата, т.е. от m-тата микрооперация, имаща продължителност 6Т.
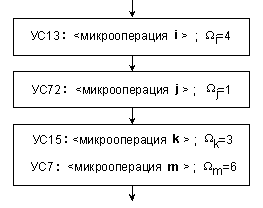
Фиг.
5.4.1. Примерна
продължителност
на
микротактовете
Тривиалното
реализиране
на
изложената
идея в
класическите
микропрограмни
структури
представлява W-кратно
последователно
записване на
една и съща
микро-команда. За
примера от
фигура 5.4.1, за
първата
микрокоманда
например,
реализацията
може да се
постигне
чрез 4-ри
кратното й
записване в 4
последователни
клетки на
микропрограмната
памет (с
адреси от a до (a+3)
включително),
по начина,
показан в
следващата
таблица.
Таблица
5.4.1.
Програмиране
на разгънат цикъл
|
№
на такта |
адрес
в МПП |
МК |
сигнал |
|
1 |
a: |
i-та
микрокоманда |
УС13 |
|
2 |
a+1: |
i-та
микрокоманда |
УС13 |
|
3 |
a+2: |
i-та
микрокоманда |
УС13 |
|
4 |
a+3: |
i-та
микрокоманда |
УС13 |
Така последователно изпълняваните микрокоманди, извличани от последователни клетки, ще реализират за управляващия сигнал УС13 необходимата продължителност от 4Т. Тази реализация не изисква изменения в структурата на микропрограмния автомат. Единственият й недостатък е, че удължава текста на микропрограмата, което води до увеличаване обема на микропрограмната памет. И още, този вариант не е достатъчно гъвкав в случай, че се наложи изменение на вече реализираната продължителност.
Идеята,
която
реализираме
тук, е
следната: необходимият
брой
повторения
на дадена микрокоманда
във времето
организираме
във вид на цикъл
от вида с
предварително
известен
брой повторения
(W на брой) на
елементарни
микротактове
с продължителност
Т. Тъй като
продължителността
на всяка
микрооперация
се определя
от конструктора,
т.е. от програмиста,
нейната
оценка в
лицето на
числото W,
следва да се
намира в
отделно поле
на структурата
на
микрокомандата.
Тъй като
всяка микрокоманда
престоява в
регистъра на
микрокомандата
поне един
елементарен
такт, то в това
поле следва
да се записва
в същност
числото (W-1).
Тази
стойност ще
се използва
като начална
за един
декрементен
брояч, с
чиято помощ
се реализира
условието за
край на микротакта.
Когато
броячът се
нулира
трябва да се
реализират
две събития:
- Да
се прекрати
изваждането
от брояча и;
- В
регистъра
на
микрокомандата
да се зареди
следващата
микрокоманда.
Импулсите
(-1) следва да се
“изрежат” от
тактовата
последователност
с помощта на
условието
![]()
където EQ=1,
когато (Бр.ЕТ)=0,
а
записващият
следващата
микрокоманда
сигнал, чрез
условието
![]()
Изказаните съображения са реализирани в логическата структура на микропрограмно управляващо устройство, представена на фигура 5.4.2.
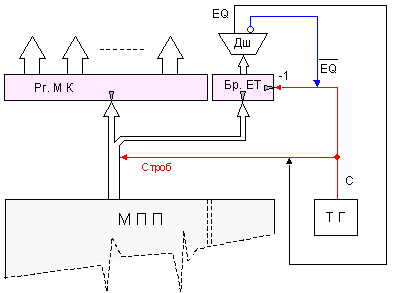
Фиг.
5.4.2. Логическа
структура за
реализация
на променлив
микротакт
Изобразеният
редом с
регистъра на
микрокомандата
брояч на
елементарните
тактове Бр.ЕТ,
всъщност е
част от
самата
микрокоманда,
т.е. от
състава на
регистъра на
микрокомандата.
Неговата
дължина се
определя
така, че да е
възможно
представянето
и на
най-голямото
от числата (W-1), възможно
за дадения
алгоритъм
![]()
Инверсната
фаза ![]() на
признака за
нулево
съдържание на
брояча на
елементарни
тактове Бр.ЕТ
маскира
постъпващите
от тактовия
генератор
импулси на
изваждащия
му вход, а
правата му
стойност EQ
маскира
тактовата
последователност
при достъпа й
към
регистъра на
микрокомандите
Рг.МК.
По този начин
в Рг.МК
се записва
следваща
микрокоманда
само когато
признакът EQ=1
и тя
престоява в
него, докато Бр.ЕТ
не се нулира.
на
признака за
нулево
съдържание на
брояча на
елементарни
тактове Бр.ЕТ
маскира
постъпващите
от тактовия
генератор
импулси на
изваждащия
му вход, а
правата му
стойност EQ
маскира
тактовата
последователност
при достъпа й
към
регистъра на
микрокомандите
Рг.МК.
По този начин
в Рг.МК
се записва
следваща
микрокоманда
само когато
признакът EQ=1
и тя
престоява в
него, докато Бр.ЕТ
не се нулира.
Тук
сме приели,
че
превключванията
на логическите
възли ще се
осъществяват
синхронно по задния
фронт на
импулсите от
тактовия генератор.
Това
означава, че
при запис в Рг.МК и в
Бр.ЕТ по
сигнала “Строб”, тяхното ново
съдържание
се появява на
техните
изходи по
неговия
заден фронт.
Такова е и
превключването
на брояча
Бр.ЕТ при
постъпване
на входните
импулси (-1).
Всяко ново
състояние,
резултат от
постъпване
на входен
импулс, се
появява по
неговия
заден фронт. Този
процес на
превключване
подробно е представен
чрез
времедиаграмата
от фигура 5.4.3. На
времедиаграмата
е изобразен
временен участък
от три
последователни
микротакта
при функционирането
на
микропрограма,
съдържаща микрооперациите,
представени
на фигура 5.4.1.
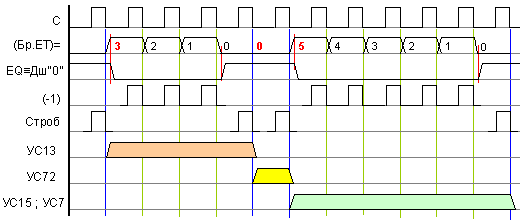
Фиг.
5.4.3. Времедиаграма
на
микротактове
с различна
продължителност
В
първия такт
микрокомандата
издава
управляващия
сигнал УС13,
който е с
продължителност
4 елементарни
такта (W=4).
Началната
стойност за
брояча (W-1)=3,
намираща се в
микрокомандата,
се записва в Бр.ЕТ
по задния
фронт на
сигнала “Строб”. В
същото време
пропада
признакът EQ,
тъй като записаното
съдържание в
брояча е
различно от нула.
Едновременно
с това
възниква
неговата
инверсна
фаза, която
разрешава
изваждащия
вход на
брояча. Така
започва
намаляване на
неговото
съдържание
до пълното му
нулиране,
когато
логическите
стойности на
двете фази на
признака EQ
отново се
сменят и
процесът се
повтаря.
Вторият
микротакт е с
продължителност
един
елементарен
такт (W=1) и
началната
стойност,
която се
записва в Бр.ЕТ е
нула. Тази,
втора по ред
микрокоманда,
издава
управляващия
сигнал УС72, а
следващата микрокоманда
издава
управляващите
сигнали УС15 и
УС7, които са с
продължителност
6Т (W=6).
Онова,
което следва
да се поясни
още, се отнася
до
изпълнението
на адресните
изчисления и
адресните
преходи.
Всъщност
апаратурата,
която
управлява
продължителността
на
микротакта,
няма никакво
отношение
към формирането
на адреса на
следващата
микрокоманда,
ето защо на
фигура 5.4.2 е
изобразена само
тя. Онази
част от
логическата
структура на
управляващото
устройство,
която е отговорна
за
формирането
на адреса на
следващата
микрокоманда,
т.е. е
отговорна за
изпълнението
на
съответния
алгоритмичен
преход,
трябва само
да успява да
изпълни
своята задача
доста преди
пристигането
на сигнала “Строб”
на
записващия
вход на Рг.МК. Този
сигнал
трябва да
заварва вече
прочетената
от
микропрограмната
памет МПП
микрокоманда,
за да може да
я фиксира по
задния си
фронт
надеждно в Рг.МК. На
практика
обаче има
реална
елементна база,
в която
реализираните
регистри или
броячи, се
превключват
по предните
фронтове на
въздействащите
им сигнали -
управляващи
и входни. Ето
защо
представяме
схема, която
е
синтезирана
при тези
изисквания.
Този вариант
на решението
е представен
чрез
логическата
структура от
фигура 5.4.4 и
чрез
времедиаграмата
за нейното
функциониране
на фигура 5.4.5.
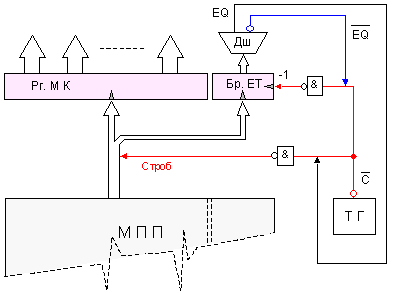
Фиг.
5.4.4. Логическа
структура с
възли,
превключващи
се по преден
фронт
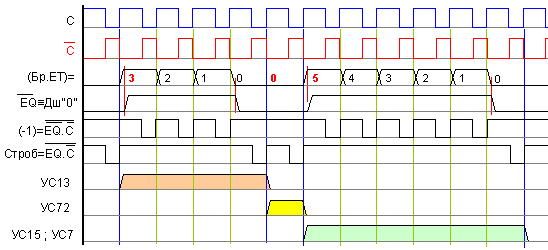
Фиг.
5.4.5. Времедиаграма
при
превключване
от предни
фронтове
Декрементните импулси (-1) следва да се “изрежат” от тактовата последователност чрез условието
![]()
където EQ=1, когато (Бр.ЕТ)=0, а
записващият
следващата
микрокоманда
сигнал – чрез
условието
![]()
Представеното
тук решение
на задачата
за реализация
на идеята за
асинхронно
управление
не е единствено.
Заключение
В този последен раздел, в духа на целия дисертационен труд, е представен синтезът и изследването на оригинална логическа структура на синхронен микропрограмен автомат, работещ с променлива продължителност на микротакта. Такива автомати също могат да бъдат определени като апериодични. Синтезираната логическата структура е обща и може да се използва като метод за проектиране на конкретни автомати с програмно закрепена логика, използващи както с естествена така и с принудителна адресация.
5.5.
Заключителни
бележки по
глава 5
В тази
глава са
получени
следните
обобщени
резултати:
Предложени
и изследвани
са логически
схеми,
реагиращи на
събития. Тези
средства за асинхронно
управление
са обобщени чрез
представянето
им само с
логически елементи,
което
позволява
регулиране
на техните
параметри по
време на
синтеза в
рамките на
една
автоматизирана
технологична
среда и
изключва
необходимостта
от регулиране
на ниво
електронни
елементи.
1.1. Детектори
на преден, на
заден и на последователни
фронтове;
1.2.
Симетрични
и
асиметрични
закъснителни
вериги. В
това число
инвертиращи
и неинвертиращи;
1.3.
Закъснителни
вериги само
на преден и
само на заден
фронт;
1.4.
Комбинирани
симетрични и
асиметрични
закъснителни
вериги;
1.5. Логическа
схема за край
на тригерно
превключване;
1.6. Логически
схеми на
синхронизатори
на асинхронни
със
синхронни
сигнали;
1.7. Логически
схеми за
асинхронен
селектор на
единичен
импулс.
Синтезирана и изследвана е оригинална логическа структура на апериодичен автомат с апаратно закрепена логика. Продължителността на всеки микротакт се формира като функция от кода на новото състояние чрез шифрираща схема.
Синтезирани са логически структури за реализация на апериодични нанокоманди и на пикокоманди в рамките на микротакта на автомата.
Синтезирани са две логически структури на апериодичен автомат с програмно закрепена логика.
Синтезираните
логически
схеми от
глава 5 са
напълно
оригинални и
технически
реализации с
тяхно
използване
принадлежат
на автора.